题目内容
9.已知平行四边形的一边为2,则下列数据中,能分别作为它的两条对角线长的是( )| A. | 8,6 | B. | 10,12 | C. | 20,6 | D. | 12,12 |
分析 可由三角形的一边与平行四边形对角线的一半组成一三角形,在三角形中利用三角形三边关系求解即可.
解答 解:如图所示,
则可在△AOB中求解,
假设AB=2,
则$\frac{1}{2}$(AC+BD)>AB,$\frac{1}{2}$(AC-BD)<AB,
而对于选项C、D来说,不符合题意,选项B中,5,6,2组不成三角形,故该选项错误;
故选A.
点评 此题考查了平行四边形的性质:平行四边形的对角相互相平分.还考查了三角形的三边关系:三角形中任意两边之和大于第三边,任意两边之差小于第三边.

练习册系列答案
相关题目
19.某商场购进了一批单价为5元的日用商品,如果以单价7元销售,每天可售出160件,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件,设这种商品的销售单价为x元,商场每天销售这种商品y件
(1)给定x的一些值,请计算y的值,填在表中
(2)求y与x之间的函数关系式;
(3)当商品的销售单价定为多少元时,该商品销售这种商品能获得的利润为420元?这时每天销售的商品是多少件?
(1)给定x的一些值,请计算y的值,填在表中
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | 160 | 140 | 120 | 100 | 80 | … |
(3)当商品的销售单价定为多少元时,该商品销售这种商品能获得的利润为420元?这时每天销售的商品是多少件?
4.为了打造区域中心城市,实现城市跨越发展,我市新区建设正按投资计划有序进行.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖土石方540m3,现决定向某大型机械租赁公司租甲、乙两种型号的挖掘机来完成这些工作,租赁公司提供的挖掘机有关信息如表:
若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
| 挖掘土石方量(单位:m/台时) | |
| 甲型挖掘机 | 60 |
| 乙型挖掘机 | 80 |
14.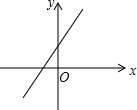 如图是一次函数y=ax-b的图象,则下列判断正确的是( )
如图是一次函数y=ax-b的图象,则下列判断正确的是( )
 如图是一次函数y=ax-b的图象,则下列判断正确的是( )
如图是一次函数y=ax-b的图象,则下列判断正确的是( )| A. | a>0,b<0 | B. | a>0,b>0 | C. | a<0,b<0 | D. | a<0,b>0 |
1.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+y=16}\\{5x=3y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2(x-y)=1}\\{3x=m-4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=\frac{1}{x}}\\{x-y=2}\end{array}\right.$ |
18.已知|a-6|+$\sqrt{b-8}$+(c-10)2=0,则这个三角形中最长的边上的高线为( )
| A. | 4 | B. | $\frac{24}{5}$ | C. | $\frac{40}{3}$ | D. | $\frac{15}{2}$ |
19.已知点(-2,y1),(-1,y2),(1,y3)都在直线y=-3x+2上,则y1,y2,y3的值的大小关系是( )
| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y3>y1>y2 | D. | y1>y2>y3 |
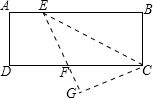 如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.
如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.