题目内容
17.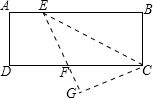 如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.
如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.
分析 由于AB∥CD,那么∠DFE=∠BEF,即可得到∠BEF的度数,由折叠的性质知:∠BEC的度数是∠BEF的一半,进而可在Rt△BEC中,根据互余角的性质求得∠BCE的度数.
解答 解:∵四边形ABCD是长方形,
∴AB∥CD,∠B=90°,
∴∠BEF=∠DFE=80°,
根据折叠的性质知:∠BEC=∠FEC=40°,
∴∠BCE=90°-∠BEC=50°.
故答案为:50°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
相关题目
7.若方程组$\left\{\begin{array}{l}{x+y=1}\\{2x+ay=b}\end{array}\right.$有唯一解,那么a,b的值应当是( )
| A. | a≠2,b为任意实数 | B. | a=2,b≠0 | C. | a=2,b≠2 | D. | a,b为任意实数 |
9.已知平行四边形的一边为2,则下列数据中,能分别作为它的两条对角线长的是( )
| A. | 8,6 | B. | 10,12 | C. | 20,6 | D. | 12,12 |
6.下面四个几何体中,俯视图是圆的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

 如图,在Rt△ABC中,∠ABC=90°.
如图,在Rt△ABC中,∠ABC=90°.