题目内容
20.(1)$2\sqrt{12}-3\sqrt{\frac{1}{3}}+\sqrt{48}-2\sqrt{3}$;(2)$(\frac{{\sqrt{3}}}{3}-\sqrt{2})(\frac{{\sqrt{2}}}{2}+\sqrt{3})$.
分析 (1)先化简,再进一步合并即可;
(2)利用二次根式的乘法展开计算化简,进一步合并即可.
解答 解:(1)原式=4$\sqrt{3}$-$\sqrt{3}$+4$\sqrt{3}$-2$\sqrt{3}$
=5$\sqrt{3}$;
(2)原式$\frac{\sqrt{6}}{6}$+1-1-$\sqrt{6}$
=$\frac{5}{6}$$\sqrt{6}$.
点评 此题考查二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
9.已知平行四边形的一边为2,则下列数据中,能分别作为它的两条对角线长的是( )
| A. | 8,6 | B. | 10,12 | C. | 20,6 | D. | 12,12 |
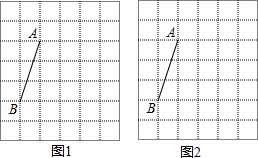 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
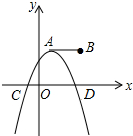 如图,点A,B的坐标分别为(1,3)和(5,3),抛物线y=a(x-h)2+k的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为9.
如图,点A,B的坐标分别为(1,3)和(5,3),抛物线y=a(x-h)2+k的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为9. 如图,在Rt△ABC中,∠ABC=90°.
如图,在Rt△ABC中,∠ABC=90°. 在生活中,我们常常看到在电线杆的两侧拉有两根钢线用来固定电线杆(如图所示),这样做的数学原理是三角形的稳定性.
在生活中,我们常常看到在电线杆的两侧拉有两根钢线用来固定电线杆(如图所示),这样做的数学原理是三角形的稳定性.