题目内容
13. 如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )| A. | 15 | B. | 13 | C. | 12 | D. | 10 |
分析 连接OB,由直径CD⊥AB于点E,得到BE=$\frac{1}{2}$AB=12,根据勾股定理得到结论.
解答  解:连接OB,
解:连接OB,
∵直径CD⊥AB于点E,
∴BE=$\frac{1}{2}$AB=12,
∴OB=$\sqrt{O{E}^{2}+B{E}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴⊙O的半径为13,
故选13.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.在3,2,-1,-4这四个数中,比-2小的数是( )
| A. | -4 | B. | -1 | C. | 2 | D. | 3 |
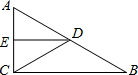 如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12.
如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12.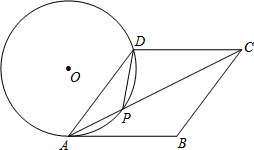 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆,若AC=8,sin∠DAC=$\frac{1}{2}$,则⊙的半径为$\frac{8}{3}$.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆,若AC=8,sin∠DAC=$\frac{1}{2}$,则⊙的半径为$\frac{8}{3}$. 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.