题目内容
18.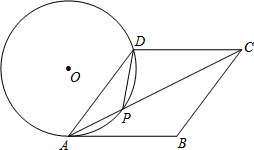 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆,若AC=8,sin∠DAC=$\frac{1}{2}$,则⊙的半径为$\frac{8}{3}$.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆,若AC=8,sin∠DAC=$\frac{1}{2}$,则⊙的半径为$\frac{8}{3}$.
分析 连结BD交AC于点F,连接OA、OP,OP交AD于E,根据菱形的性质得DB与AC互相垂直平分,则AF=4,解直角三角形求出DF,根据垂径定理求出AE=DE,OP⊥AD,解直角三角形求出PE,根据勾股定理得出关于R的方程,求出R即可.
解答 解:连结BD交AC于点F,连接OA、OP,OP交AD于E,如图,
∵四边形ABCD为菱形,
∴DB与AC互相垂直平分,
∵AC=8,sin∠DAC=$\frac{1}{2}$,
∴AF=4,sin∠DAC=$\frac{DF}{AD}$=$\frac{1}{2}$,
由勾股定理得:(2DF)2-42=DF2,
∴DF=$\frac{4\sqrt{3}}{3}$,
∴AD=$\frac{8\sqrt{3}}{3}$,
∵AP=PD,
∴$\widehat{AP}$=$\widehat{PD}$,
∵OP为半径,
∴AE=DE,OP⊥AD,
∴AE=$\frac{1}{2}$AD=$\frac{4\sqrt{3}}{3}$,
在Rt△PAE中,sin∠1=$\frac{PE}{AP}$=$\frac{1}{2}$,
∴PE=$\frac{4}{3}$,
设⊙O的半径为R,则OE=R-$\frac{4}{3}$,OA=R,
在Rt△OAE中,∵OA2=OE2+AE2,
∴R2=(R-$\frac{4}{3}$)2+( $\frac{4\sqrt{3}}{3}$)2,
∴R=$\frac{8}{3}$,
即⊙O的半径$\frac{8}{3}$,
故答案为:$\frac{8}{3}$.
点评 本题考查了解直角三角形,菱形的性质和锐角三角函数以及勾股定理的应用,能灵活运用定理进行推理和计算是解此题的关键.

练习册系列答案
相关题目
13. 如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
 如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )| A. | 15 | B. | 13 | C. | 12 | D. | 10 |
7.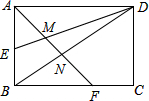 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )| A. | $\frac{2\sqrt{2}}{5}$ | B. | $\frac{9\sqrt{2}}{20}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{4\sqrt{2}}{5}$ |
8.已知圆锥的底面半径为4cm,母线长为6cm,则它的侧面展开图的面积等于( )
| A. | 24cm2 | B. | 48cm2 | C. | 24πcm2 | D. | 12πcm2 |
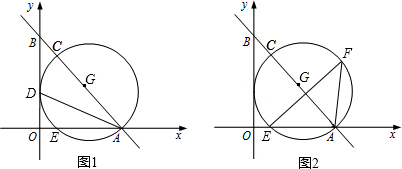
 如图,在等腰△ABC中,AB=AC,AD⊥BC,∠BAC=50°,则∠BAD=25°.
如图,在等腰△ABC中,AB=AC,AD⊥BC,∠BAC=50°,则∠BAD=25°. 如图,⊙O的直径AB⊥弦CD,垂足为点E,连接AC,若CD=2$\sqrt{3}$,∠A=30°,则⊙O的半径为2.
如图,⊙O的直径AB⊥弦CD,垂足为点E,连接AC,若CD=2$\sqrt{3}$,∠A=30°,则⊙O的半径为2.


