题目内容
5.计算(1)$\frac{2x}{x+1}+\frac{2}{x+1}$
(2)a-1-$\frac{{a}^{2}}{a+1}$.
分析 (1)同分母分式加减法法则:同分母的分式相加减,分母不变,把分子相加减;
(2)异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.
解答 解:(1)$\frac{2x}{x+1}+\frac{2}{x+1}$
=$\frac{2x+2}{x+1}$
=2;
(2)a-1-$\frac{{a}^{2}}{a+1}$
=$\frac{{a}^{2}-1}{a+1}$-$\frac{{a}^{2}}{a+1}$
=-$\frac{1}{a+1}$.
点评 考查了分式加减法,注意:①分式的通分必须注意整个分子和整个分母,分母是多项式时,必须先分解因式,分子是多项式时,要把分母所乘的相同式子与这个多项式相乘,而不能只同其中某一项相乘. ②通分是和约分是相反的一种变换.约分是把分子和分母的所有公因式约去,将分式化为较简单的形式;通分是分别把每一个分式的分子分母同乘以相同的因式,使几个较简单的分式变成分母相同的较复杂的形式.约分是对一个分式而言的;通分则是对两个或两个以上的分式来说的.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
16.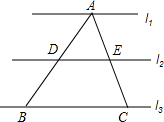 如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
 如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
13. 如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
 如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )| A. | 15 | B. | 13 | C. | 12 | D. | 10 |
20.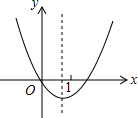 已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )
已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )
 已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )
已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=( )| A. | a+b | B. | a-2b | C. | a-b | D. | 3a |
17.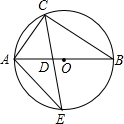 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )| A. | 1:$\sqrt{2}$ | B. | 1:$\sqrt{3}$ | C. | 1:2 | D. | 2:3 |
14.为了让书籍开拓学生的视野,陶冶学生的情操,向阳中学开展了“五个一”课外阅读活动,为了解全校学生课外阅读情况,抽样调查了50名学生平均每天课外阅读时间(单位:min),将抽查得到的数据分成5组,下面是尚未完成的频数、频率分布表:
(1)将表中空格处的数据补全,完成上面的频数、频率分布表;
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
| 组别 | 分组 | 频数(人数) | 频率 |
| 1 | 10≤t<30 | 0.16 | |
| 2 | 30≤t<50 | 20 | |
| 3 | 50≤t<70 | 0.28 | |
| 4 | 70≤t<90 | 6 | |
| 5 | 90≤t<110 |
(2)请在给出的平面直角坐标系中画出相应的频数直方图;
(3)如果该校有1500名学生,请你估计该校共有多少名学生平均每天阅读时间不少于50min?
15.人体中红细胞的直径约为0.0000077m,将数0.0000077用科学记数法表示为( )
| A. | 77×10-5 | B. | 0.77×10-7 | C. | 7.7×10-6 | D. | 7.7×10-7 |




