题目内容
1.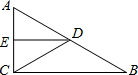 如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12.
如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12.
分析 首先利用勾股定理求得BC的长,易证DE是△ABC的中位线,然后依据三角形的中位线定理即可求解.
解答 解:在直角△ABC中,
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC=4,AE=3,AD=5,
∴△AED的周长=AE+AD+ED=3+5+4=12
故答案是:12.
点评 本题考查了勾股定理、三角形的中位线定理,正确证明DE是中位线是关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
11. 如图,点D、E、F分别为△ABC的三边的中点,若△DEF的周长是10,则△ABC的周长是( )
如图,点D、E、F分别为△ABC的三边的中点,若△DEF的周长是10,则△ABC的周长是( )
 如图,点D、E、F分别为△ABC的三边的中点,若△DEF的周长是10,则△ABC的周长是( )
如图,点D、E、F分别为△ABC的三边的中点,若△DEF的周长是10,则△ABC的周长是( )| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
16.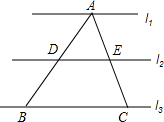 如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
 如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
13. 如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
 如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )
如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为( )| A. | 15 | B. | 13 | C. | 12 | D. | 10 |
11.现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,EF=4,则CD=4.
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,EF=4,则CD=4.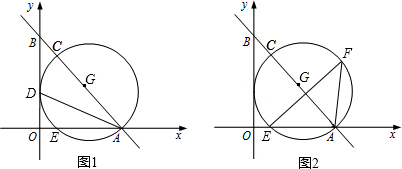
 如图,在等腰△ABC中,AB=AC,AD⊥BC,∠BAC=50°,则∠BAD=25°.
如图,在等腰△ABC中,AB=AC,AD⊥BC,∠BAC=50°,则∠BAD=25°.


