题目内容

3．先化简，再求值：（$\frac{x}{x-3}$-$\frac{1}{x-3}$）÷$\frac{{x}^{2}-1}{{x}^{2}-6x+9}$，其中x满足2x+4=0．

分析 原式括号中利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，求出已知方程的解得到x的值，代入计算即可求出值．

解答 解：原式=$\frac{x-1}{x-3}$•$\frac{（x-3）^{2}}{（x+1）（x-1）}$=$\frac{x-3}{x+1}$，
由2x+4=0，得到x=-2，
则原式=5．

点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
13．如图，AB是⊙O的一条弦，直径CD⊥AB于点E．若AB=24，OE=5，则⊙O的半径为（　　）
A．15B．13C．12D．10
14．为了让书籍开拓学生的视野，陶冶学生的情操，向阳中学开展了“五个一”课外阅读活动，为了解全校学生课外阅读情况，抽样调查了50名学生平均每天课外阅读时间（单位：min），将抽查得到的数据分成5组，下面是尚未完成的频数、频率分布表：
 组别 分组 频数（人数） 频率
 1 10≤t＜30  0.16
 2 30≤t＜50 20 
 3 50≤t＜70  0.28
 4 70≤t＜90 6 
 5 90≤t＜110  
（1）将表中空格处的数据补全，完成上面的频数、频率分布表；
（2）请在给出的平面直角坐标系中画出相应的频数直方图；
（3）如果该校有1500名学生，请你估计该校共有多少名学生平均每天阅读时间不少于50min？
11．现有两枚质地均匀的正方体骰子，每枚骰子的六个面上都分别标有数字1、2、3、4、5、6．同时投掷这两枚骰子，以朝上一面所标的数字为掷得的结果，那么所得结果之和为9的概率是（　　）
A．$\frac{1}{3}$B．$\frac{1}{6}$C．$\frac{1}{9}$D．$\frac{1}{12}$
18．若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（　　）
A．7B．10C．35D．70
8．已知圆锥的底面半径为4cm，母线长为6cm，则它的侧面展开图的面积等于（　　）
A．24cm2B．48cm2C．24πcm2D．12πcm2
15．人体中红细胞的直径约为0.0000077m，将数0.0000077用科学记数法表示为（　　）
A．77×10-5B．0.77×10-7C．7.7×10-6D．7.7×10-7
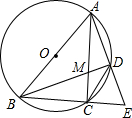12．先化简，再求值：$\frac{a}{a-b}$（$\frac{1}{b}$-$\frac{1}{a}$）+$\frac{a-1}{b}$，其中a=2，b=$\frac{1}{3}$．
1．如图，△ABC内接于⊙O，AB是⊙O的直径，点D是劣弧AC上的一点，连结AD并延长与BC的延长线交于点E，AC、BD相交于点M．
（1）求证：BC•CE=AC•MC；
（2）若点D是劣弧AC的中点，tan∠ACD=$\frac{1}{3}$，MD•BD=10，求⊙O的半径．
（3）若CD∥AB，过点A作AF∥BC，交CD的延长线于点F，求$\frac{CF}{CD}$-$\frac{BC}{CE}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网