题目内容
14.计算:①(-1)3+$\sqrt{8}$+($\sqrt{2}$-1)0-$\sqrt{2}$.
②解分式方程:$\frac{3}{{x}^{2}-9}$+$\frac{x}{x-3}$=1.
分析 (1)利用零指数幂的性质和二次根式的性质化简各数求出即可;
(2)首先找出最简公分母,进而去分母化简求出即可.
解答 解:(1)原式=-1+2$\sqrt{2}$+1-$\sqrt{2}$
=$\sqrt{2}$;
(2)去分母得:3+x(x+3)=x2-9,
解得:x=-4,
检验:当x=-4时,x2-9≠0,故x=-4是原方程的根.
点评 此题主要考查了实数运算以及解分式方程,正确掌握相关性质化简各数是解题关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
2.下列命题中,假命题是( )
| A. | 方差是衡量一组数据波动大小的统计量 | |
| B. | 影响鞋店进货时决策的主要统计量是众数 | |
| C. | 对角线互相垂直且相等的四边形是正方形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
9.我国第六次全国人口普查数据显示,居住在城镇的人口总数大约为6 6600 0000人,用科学记数法表示为( )
| A. | 66.6×107 | B. | 6.66×108 | C. | 6.66×107 | D. | 0.666×109 |
4.在一个不透明的袋子中装有红、黄两种颜色的球共20个,每个球除颜色外完全相同.某学习兴趣小组做摸球实验,将球搅匀后从中随机摸出1个球,记下颜色后再放回袋中,不断重复.下表是活动进行中的部分统计数据.
(1)完成上表;
(2)“摸到红球”的概率的估计值是0.6(精确到0.1)
(3)试估算袋子中红球的个数.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到红球的次数m | 59 | 96 | 118 | 290 | 480 | 601 |
| 摸到红球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.58 | 0.60 | 0.601 |
(2)“摸到红球”的概率的估计值是0.6(精确到0.1)
(3)试估算袋子中红球的个数.
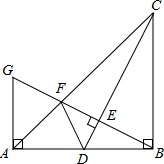 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G.
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G.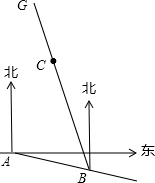 如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.
如图所示,某工程队要在一社区点C处修建一条小路CE,使小路CE与AB方向一致.