题目内容
4.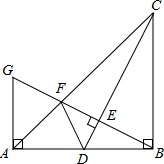 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G.
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G.(1)求$\frac{AF}{AC}$的值;
(2)求$\frac{{S}_{△AFG}}{{S}_{△ABC}}$的值.
分析 (1)根据等角的余角相等得到∠DBE=∠BCD,由于AB=CB,点D是AB的中点,得到BD=$\frac{1}{2}$AB=$\frac{1}{2}$CB,求出tan∠BCD=$\frac{BD}{BC}$=$\frac{1}{2}$在Rt△ABG中,tan∠DBE=$\frac{AG}{AB}$=$\frac{1}{2}$,推出△AFG∽△CFB,即可得到结论;
(2)由(1)证得△AFG∽△CFB,根据相似三角形的性质得到$\frac{{S}_{△AFG}}{{S}_{△BCF}}$=($\frac{1}{2}$)2=$\frac{1}{4}$,由于$\frac{AF}{AB}$=$\frac{1}{3}$,得到$\frac{CF}{AB}$=$\frac{2}{3}$,于是得到$\frac{{S}_{△AFG}}{{S}_{△ABC}}$=$\frac{\frac{1}{4}×\frac{2}{3}{S}_{△ABC}}{{S}_{△ABC}}$=$\frac{1}{6}$.
解答 解:(1)∵∠ABC=90°,BG⊥CD,
∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
∴∠DBE=∠BCD,
∵AB=CB,点D是AB的中点,
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}$CB,
∵tan∠BCD=$\frac{BD}{BC}$=$\frac{1}{2}$
∴在Rt△ABG中,tan∠DBE=$\frac{AG}{AB}$=$\frac{1}{2}$,
∵BC⊥AB,AG⊥AB,
∴AG∥BC,
∴△AFG∽△CFB,
∴AF:CF=AG:BC=1:2,
∴AF=$\frac{1}{3}$AC,
∴$\frac{AF}{AC}$=$\frac{1}{3}$;
(2)由(1)证得△AFG∽△CFB,
∴$\frac{{S}_{△AFG}}{{S}_{△BCF}}$=($\frac{1}{2}$)2=$\frac{1}{4}$,
∵$\frac{AF}{AB}$=$\frac{1}{3}$,
∴$\frac{CF}{AB}$=$\frac{2}{3}$,
∴S△BCF=$\frac{2}{3}$S△ABC,
∴$\frac{{S}_{△AFG}}{{S}_{△ABC}}$=$\frac{\frac{1}{4}×\frac{2}{3}{S}_{△ABC}}{{S}_{△ABC}}$=$\frac{1}{6}$.
点评 此题考查了相似三角形的判定与性质、直角三角形的性质以及三角函数等知识.此题难度适中,解题的关键是证得△AFG∽△CFB,注意掌握数形结合思想与转化思想的应用.

 关于x的不等式-2x+a≥5的解集如图所示,则a的值是3.
关于x的不等式-2x+a≥5的解集如图所示,则a的值是3. 如图,D为△ABC内的一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为24.
如图,D为△ABC内的一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为24.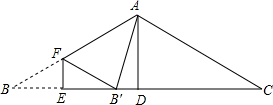 如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.
如图,△ABC中,AB=AC,∠BAC=120°,BC=6,AD⊥BC,垂足为D.E是BC上一动点,EF⊥BC,交AB于F,把∠B沿EF折叠,使点B落在点B′处.当△AB′F为直角三角形时,BE=1.