题目内容
9.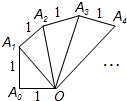 如图中的螺旋由一系列直角三角形组成,∠OA0A1,∠OA1A2,∠OA2A3,…为90°,OA0,A0A1,A1A2…为1,则△OAn-1An的面积为$\frac{\sqrt{n}}{2}$.
如图中的螺旋由一系列直角三角形组成,∠OA0A1,∠OA1A2,∠OA2A3,…为90°,OA0,A0A1,A1A2…为1,则△OAn-1An的面积为$\frac{\sqrt{n}}{2}$.
分析 分别求出直角三角形的面积进而得出变化规律即可得出答案.
解答 解:∵OA0=A0A1=A1A2=…=1,
∴第1个直角三角形的面积为:$\frac{1}{2}$,
第2个直角三角形的面积为:$\frac{1}{2}$×$\sqrt{2}$×1=$\frac{\sqrt{2}}{2}$,
第3个直角三角形的面积为:$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
…
∴△OAn-1An的面积即为第n个三角形面积为:$\frac{\sqrt{n}}{2}$,
故答案为:$\frac{{\sqrt{n}}}{2}$.
点评 此题主要考查了勾股定理以及三角形面积求法,正确得出三角形面积变化规律是解题关键.

练习册系列答案
相关题目
17.下列叙述中正确的是( )
| A. | 一个数的倒数总是比它本身小 | B. | 任何自然数都有倒数 | ||
| C. | 一个数a乘以真分数,积一定小于a | D. | 如果a×b=1,则a与b互为倒数 |
4.某地今年10月份某一周的日最高气温(单位:℃)分别为22,21,18,20,19,18,15,则这周的日最高气温的平均值为( )
| A. | 18℃ | B. | 19℃ | C. | 20℃ | D. | 21℃ |
1.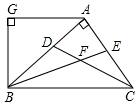 如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:
如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:
①∠BAG=2∠ABE;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.
其中正确的结论是( )
 如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:
如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABE;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.
其中正确的结论是( )
| A. | ①③④ | B. | ②④ | C. | ①③ | D. | ①②③④ |
19.若(m-n)(m-n-2)-8=0,则m-n的值为( )
| A. | 4或-2 | B. | 4 | C. | -2 | D. | 2 |
 如图,在菱形ABCD中,CE垂直对角线AC于点C,AB的延长线交CE于点E.
如图,在菱形ABCD中,CE垂直对角线AC于点C,AB的延长线交CE于点E.
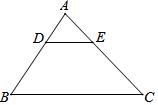 已知:如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=2,AB=6,求DE:BC的值.
已知:如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=2,AB=6,求DE:BC的值.