题目内容
20.(1)如图(1)所示,已知在△ABC中,O为∠ABC和∠ACB的平分线BO,CO的交点.试猜想∠BOC和∠A的关系,并说明理由.(2)如图(2)所示,若O为∠ABC的平分线BO和∠ACE的平分线CO的交点,则∠BOC与∠A的关系又该怎样?为什么?
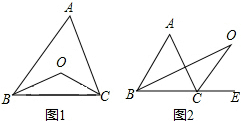
分析 (1)先列出∠A、∠ABC、∠ACB的关系,再列出∠BOC、∠OBC、∠OCB的关系,然后列出∠ABC和∠OBC、∠ACB和∠OCB的关系,进而得出结论;
(2)列出∠A、∠ABC、∠ACE的关系,再列出∠OBC、∠O、∠OCE的关系,然后列出∠ABC和∠OBC、∠ACE和∠OCE的关系,进而得出结论.
解答 解:(1)∠BOC=$\frac{1}{2}$∠A+90°.
理由如下:
在△ABC中,∠A+∠ABC+∠ACB=180°,在△BOC中,∠BOC+∠OBC+∠OCB=180°,
又∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠ABC=2∠OBC,∠ACB=2∠OCB.
∴∠BOC+$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=180°.
∴∠BOC=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A.
(2)∠BOC=$\frac{1}{2}$∠A.
理由如下:
∵∠A+∠ABC=∠ACE,∠OBC+∠BOC=∠OCE,
∴∠A=∠ACE-∠ABC,∠BOC=∠OCE-∠OBC
又∵BO,CO分别是∠ABC和∠ACE的平分线,
∴∠ABC=2∠OBC,∠ACE=2∠OCE.
∴∠BOC=∠OCE-∠OBC=$\frac{1}{2}$∠ACE-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠ACE-∠ABC)
=$\frac{1}{2}$∠A.
点评 本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键,读懂题目提供的信息,然后利用提供信息的思路也很重要.

练习册系列答案
相关题目
17.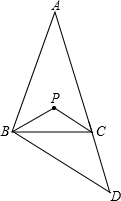 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=( )
 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=( )| A. | 105° | B. | 110° | C. | 130° | D. | 145° |

 如图,在Rt△ABC中,∠C=90°,AC=6,∠A的平分线交BC于点D,DE⊥AB于点E,且BE=4,求DE的长.
如图,在Rt△ABC中,∠C=90°,AC=6,∠A的平分线交BC于点D,DE⊥AB于点E,且BE=4,求DE的长.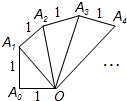 如图中的螺旋由一系列直角三角形组成,∠OA0A1,∠OA1A2,∠OA2A3,…为90°,OA0,A0A1,A1A2…为1,则△OAn-1An的面积为$\frac{\sqrt{n}}{2}$.
如图中的螺旋由一系列直角三角形组成,∠OA0A1,∠OA1A2,∠OA2A3,…为90°,OA0,A0A1,A1A2…为1,则△OAn-1An的面积为$\frac{\sqrt{n}}{2}$.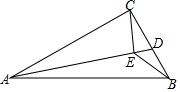 如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是$\sqrt{61}$-6cm.
如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是$\sqrt{61}$-6cm.