题目内容
14.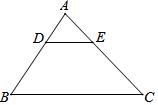 已知:如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=2,AB=6,求DE:BC的值.
已知:如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=2,AB=6,求DE:BC的值.
分析 根据平行线得出△ADE∽△ABC,根据相似得出比例式,代入求出即可.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{DE}{BC}=\frac{2}{6}=\frac{1}{3}$.
点评 本题考查了相似三角形的性质和判定,关键是求出相似后得出比例式,题目比较典型,难度适中.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
2.下列各式中,与分式$\frac{ax+ay}{{x}^{2}-{y}^{2}}$相等的是( )
| A. | $\frac{2a}{x+y}$ | B. | $\frac{a}{x+y}$ | C. | $\frac{2a}{x-y}$ | D. | $\frac{a}{x-y}$ |
19.下列函数中y=-4x,y=$\frac{x}{2}$-3,y=$\frac{x+4}{3}$,y=$\frac{2}{x}$-1,y=-x2+1,y=-2$\sqrt{x}$,y=3,3x+2y=5,其中y是x的一次函数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
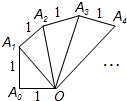 如图中的螺旋由一系列直角三角形组成,∠OA0A1,∠OA1A2,∠OA2A3,…为90°,OA0,A0A1,A1A2…为1,则△OAn-1An的面积为$\frac{\sqrt{n}}{2}$.
如图中的螺旋由一系列直角三角形组成,∠OA0A1,∠OA1A2,∠OA2A3,…为90°,OA0,A0A1,A1A2…为1,则△OAn-1An的面积为$\frac{\sqrt{n}}{2}$.