题目内容
1.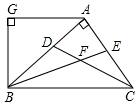 如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:
如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:①∠BAG=2∠ABE;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.
其中正确的结论是( )
| A. | ①③④ | B. | ②④ | C. | ①③ | D. | ①②③④ |
分析 根据已知条件AG∥BC,可得到∠BAG=∠ABC,再根据BE平分∠ABC,可判断出①正确;根据BG⊥AG,AB⊥AC,可得到∠GAB+∠ABG=90°,∠ABC+∠ACB=90°,再根据∠BAG=∠ABC,可判断出③正确;根据CD、BE分别是△ABC的角平分线,得到∠FBC+∠FCB=$\frac{1}{2}$(∠ABC+∠ACB),再根据三角形内角和定理得到答案.
解答 解:∵BE平分∠ABC,
∴∠ABF=∠CBF=$\frac{1}{2}$∠ABC,
∵AG∥BC,
∴∠BAG=∠ABC,
∴∠BAG=2∠ABF,
故①正确,
无法确定BA是否平分∠CBG,
故②错误;
∵BG⊥AG,
∴∠GAB+∠ABG=90°,
∴∠GBA+∠ABC=90°,
∵AB⊥AC,
∴∠ABC+∠ACB=90°,
∴∠ABG=∠ACB,
故③正确,
∵CD、BE分别是△ABC的角平分线,
∴∠EBC=$\frac{1}{2}$∠ABC,∠DCB=$\frac{1}{2}$∠ACB,
∵∠ABC+∠ACB=90°,
∴∠CFB=180°-(180°-90°)÷2=135°,
故④正确.
故选:A.
点评 此题主要考查了平行线的性质,三角形内角和定理,角平分线的性质,垂直,关键是理清角之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列实数:$\frac{π}{2}$,$\frac{22}{7}$,1.414,$\root{3}{9}$,$\sqrt{\frac{1}{2}}$,2.01010010001…,-$\sqrt{36}$中,无理数有( )个.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11. 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
 如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )
如图,菱形ABCD的一边中点M到对角线交点O的距离为5cm,则菱形ABCD的周长为( )| A. | 5cm | B. | 10cm | C. | 20cm | D. | 40cm |
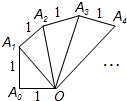 如图中的螺旋由一系列直角三角形组成,∠OA0A1,∠OA1A2,∠OA2A3,…为90°,OA0,A0A1,A1A2…为1,则△OAn-1An的面积为$\frac{\sqrt{n}}{2}$.
如图中的螺旋由一系列直角三角形组成,∠OA0A1,∠OA1A2,∠OA2A3,…为90°,OA0,A0A1,A1A2…为1,则△OAn-1An的面积为$\frac{\sqrt{n}}{2}$.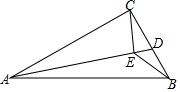 如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是$\sqrt{61}$-6cm.
如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是$\sqrt{61}$-6cm.