题目内容
7.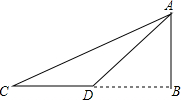 如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.
如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.
分析 利用AB表示出BC,BD.让BC减去BD等于20即可求得AB长.
解答 解:设AB的高为x米,
∵∠B=90°,∠ADB=45°,
∴BD=x,
又∵∠B=90°,∠ACB=30°,
∴$tan∠ACB=\frac{AB}{BC}$,
∴$\frac{{\sqrt{3}}}{3}=\frac{x}{20+x}$,
∴$x=10\sqrt{3}+10$.
答:AB的长为(10$\sqrt{3}$+10)米.
点评 本题主要考查了三角函数的定义,根据三角函数可以把问题转化为方程问题来解决.

练习册系列答案
相关题目
16.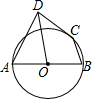 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )
 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
 如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.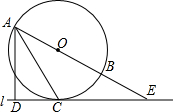 如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC. 已知有理数a,b在数轴上的位置如图所示.则a,-b,b-a,a-b这四个数的大小关系是a-b<-b<a<b-a(用“<”号依次排列)
已知有理数a,b在数轴上的位置如图所示.则a,-b,b-a,a-b这四个数的大小关系是a-b<-b<a<b-a(用“<”号依次排列)