题目内容
17. 如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.(1)求证:△ABC≌△DCB;
(2)过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,若∠AMB=70°,求∠N的度数.
分析 (1)利用SSS定理可直接判定△ABC≌△DCB;
(2)首先根据CN∥BD、BN∥AC,可判定四边形BNCM是平行四边形,再根据△ABC≌△DCB可得∠1=∠2,进而可得BM=CM,根据邻边相等的平行四边形是菱形可得结论.
解答 解:(1)在△ABC和△DCB中,
$\left\{\begin{array}{l}{AB=DC}\\{AC=DB}\\{CB=BC}\end{array}\right.$,
∴△ABC≌△DCB(SSS);
(2)∵CN∥BD、BN∥AC,
∴四边形BNCM是平行四边形,
∵△ABC≌△DCB,
∴∠1=∠2,
∴BM=CM,
∴四边形BNCM是菱形,
∴∠N=∠BMC,
∵∠AMB=70°,
∴∠N=∠BMC=110°.
点评 此题主要考查了全等三角形的判定和性质,以及菱形的判定,关键是掌握一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目

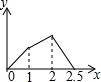
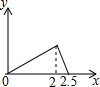
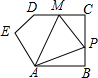 在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )
在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )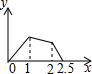
 将一副三角板按如图方式进行摆放,请判断∠1,∠2是否互补,并说明理由.
将一副三角板按如图方式进行摆放,请判断∠1,∠2是否互补,并说明理由. 完成下列各题:
完成下列各题:
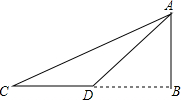 如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.
如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.