题目内容
2.我们知道,经过原点的抛物线解析式可以是y=ax2+bx(a≠0)(1)对于这样的抛物线:当顶点坐标为(1,1)时,求a、b的值;
(2)当顶点坐标为(m,2m),m≠0时,求a与m之间的关系式;
(3)继续探究,如果b≠0,且过原点的抛物线顶点在直线y=(k+1)x(k≠-1)上,请用含k的代数式表示b.
分析 (1)抛物线y=ax2+bx的顶点坐标为(-$\frac{b}{2a}$,$\frac{-{b}^{2}}{4a}$),根据题意列出方程组求解可得;
(2)根据抛物线顶点式列出方程组,将方程组中b消去可得a、m间关系;
(3)将抛物线顶点(-$\frac{b}{2a}$,$\frac{-{b}^{2}}{4a}$)代入直线解析式y=(k+1)x,整理可得.
解答 解:(1)∵顶点坐标为(1,1),
∴$\left\{\begin{array}{l}{-\frac{b}{2a}=1}\\{\frac{-{b}^{2}}{4a}=1}\end{array}\right.$,
解得:a=-1,b=2;
(2)当顶点坐标为(m,2m),m≠0时,
$\left\{\begin{array}{l}{-\frac{b}{2a}=m}\\{\frac{-{b}^{2}}{4a}=2m}\end{array}\right.$,
解得:a=-$\frac{2}{m}$;
(3)过原点的抛物线y=ax2+bx的顶点坐标为(-$\frac{b}{2a}$,$\frac{-{b}^{2}}{4a}$),
∵抛物线顶点在直线y=(k+1)x(k≠-1)上,
∴-$\frac{{b}^{2}}{4a}$=-$\frac{b}{2a}$(k+1),
整理得:b=2k+2.
点评 本题考查了二次函数性质及解方程组的能力,熟练掌握二次函数的顶点式是解题的关键.

练习册系列答案
相关题目
13.如果把(a-b)视为一个整体,化简2(a-b)2+3(b-a)2的结果是( )
| A. | -5(a-b)2 | B. | 5(b-a)2 | C. | -(a-b)2 | D. | (b-a)2 |
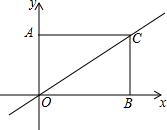 有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.
有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.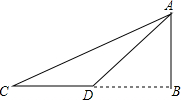 如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.
如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.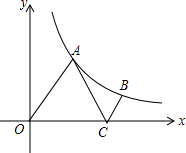 如图,点A,B在反比例函数y=$\frac{m}{x}$的图象上,点A的坐标为($\sqrt{3}$,3),点C在x轴上,且使△AOC是等边三角形,BC∥OA.
如图,点A,B在反比例函数y=$\frac{m}{x}$的图象上,点A的坐标为($\sqrt{3}$,3),点C在x轴上,且使△AOC是等边三角形,BC∥OA.