题目内容
16.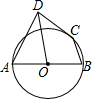 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
分析 作OM⊥AD于M,BN⊥OC于N,先证明四边形CDMO是矩形,△OAM≌△BON,得到BN=OM=CD=2,在RT△BCN中利用勾股定理求出CN,在RT△OBN中,利用勾股定理求出半径,即可解决问题.
解答 解: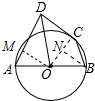 作OM⊥AD于M,BN⊥OC于N,
作OM⊥AD于M,BN⊥OC于N,
∵DC是⊙O切线,
∴DC⊥OC,
∵AD⊥CD,
∴∠DCO=∠CDM=∠OMD=90°,
∴四边形CDMO是矩形,
∴OM=CD=2,OC∥AD,
∴∠BON=∠OAM,∵∠ADO=∠DOC
在△AOM和△OBN中,
$\left\{\begin{array}{l}{∠OMA=∠BNO}\\{∠BON=∠OAM}\\{OA=OB}\end{array}\right.$,
∴△OAM≌△BON,
∴BN=OM=2,
在RT△CBN中,∵∠BNC=90°,BN=2,BC=$\sqrt{5}$,
∴CN=$\sqrt{B{C}^{2}-B{N}^{2}}=1$,设半径为r,
在RT△OBN中,∵OB2=ON2+BN2,
∴r2=4+(r-1)2,
∴r=$\frac{5}{2}$,
在RT△DOC中,tan∠DOC=tan∠ADO=$\frac{DC}{CO}$=$\frac{2}{\frac{5}{2}}$=$\frac{4}{5}$,
∴tan∠ADO=$\frac{4}{5}$,
故选C.
点评 本题考查切线的性质、矩形的判定和性质、全等三角形的判定和性质、三角函数等知识,解题的关键是添加辅助线构造全等三角形,学会常用辅助线的添加方法,属于中考常考题型.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
4.关于x的一元二次方程x2+x-1=0两根的倒数和是( )
| A. | 1 | B. | 3 | C. | 1或2 | D. | 1或3 |
7.当某一几何体在投影面P前的摆放位置确定以后,改变它与投影面P的距离,其正投影的形状( )
| A. | 不发生变化 | B. | 变大 | C. | 变小 | D. | 无法确定 |
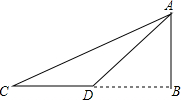 如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.
如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB. 已知:如图,A,D是直线EF上两点,∠1+∠2=180°,求证:AB∥CD.
已知:如图,A,D是直线EF上两点,∠1+∠2=180°,求证:AB∥CD.