题目内容
19.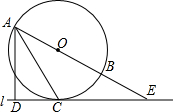 如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.(1)求证:∠DAC=∠CAE;
(2)若∠CAB=30°,CE=3$\sqrt{3}$,求⊙O的半径.
分析 (1)连结OC,如图,根据切线的性质得OC⊥CE,加上AD⊥CE,则根据平行线的判定可得OC∥AD,则∠2=∠3,然后利用等量代换可得∠1=∠2;
(2)先利用三角形外角性质可得∠COE,然后在Rt△OCE中利用三角函数计算OC的长.
解答 (1)证明:连结OC,如图,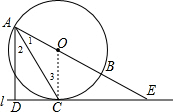
∵直线l与⊙O相切于点C,
∴OC⊥CE,
∵AD⊥CE,
∴OC∥AD,
∴∠2=∠3,
∵OC=OA,
∴∠1=∠3,
∴1=∠2,
即∠DAC=∠CAE;
(2)解:∵∠COE=∠1+∠3=2∠1=2×30°=60°,
在Rt△OCE中,∵tan∠COE=$\frac{CE}{OC}$,
∴OC=$\frac{3\sqrt{3}}{tan60°}$=3,
即⊙O的半径为3.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.解决(1)小题的关键是证明OC∥AD.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
4.关于x的一元二次方程x2+x-1=0两根的倒数和是( )
| A. | 1 | B. | 3 | C. | 1或2 | D. | 1或3 |
 完成下列各题:
完成下列各题: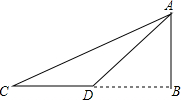 如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.
如图,在河的对岸有水塔AB,今在C处测得塔顶A的仰角为30°,前进20米后到D处,又测得A的仰角为45°,求塔高AB.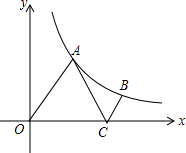 如图,点A,B在反比例函数y=$\frac{m}{x}$的图象上,点A的坐标为($\sqrt{3}$,3),点C在x轴上,且使△AOC是等边三角形,BC∥OA.
如图,点A,B在反比例函数y=$\frac{m}{x}$的图象上,点A的坐标为($\sqrt{3}$,3),点C在x轴上,且使△AOC是等边三角形,BC∥OA. 已知:如图,A,D是直线EF上两点,∠1+∠2=180°,求证:AB∥CD.
已知:如图,A,D是直线EF上两点,∠1+∠2=180°,求证:AB∥CD.