题目内容
1.已知实数a、b(a>b)都是方程x2-x-1=0的解,则$\frac{1}{a}$$-\frac{1}{b}$=$\sqrt{5}$.分析 根据根与系数的关系得到a+b=1,ab=-1,再利用完全平方公式变形得到(b-a)2=(a+b)2-4ab=5,求得b-a的值,再代入到$\frac{1}{a}$$-\frac{1}{b}$=$\frac{b-a}{ab}$可得.
解答 解:根据题意a+b=1,ab=-1,
∴(b-a)2=(a+b)2-4ab=5,
∵a>b,
∴b-a=-$\sqrt{5}$,
∴$\frac{1}{a}$$-\frac{1}{b}$=$\frac{b-a}{ab}$=$\frac{-\sqrt{5}}{-1}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
11.如果∠1与∠2的两边互相平行,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 无法确定 |
12.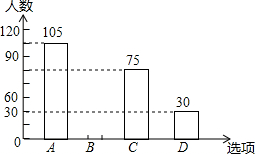 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
结合上述统计图表,回答下列问题:
(1)本次抽查的学生共300人,x=30%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请估计该校喜爱“篮球”这项球类运动的学生约有多少人?
(3)学校决定举行一次乒乓球比赛,甲,乙,丙,丁四人参加比赛,从四人中随机抽取两人打第一场比赛,请用树状图或列表法所抽到的两人恰好是甲和丁的概率.
 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:| 选项 | 球类运动 | 百分比 |
| A | 乒乓球 | 35% |
| B | 羽毛球 | x |
| C | 篮球 | 25% |
| D | 其他 | 10% |
(1)本次抽查的学生共300人,x=30%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请估计该校喜爱“篮球”这项球类运动的学生约有多少人?
(3)学校决定举行一次乒乓球比赛,甲,乙,丙,丁四人参加比赛,从四人中随机抽取两人打第一场比赛,请用树状图或列表法所抽到的两人恰好是甲和丁的概率.
 如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.
如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.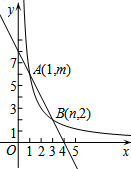 直线y=-2x+8和双曲线y=$\frac{k}{x}$(k≠0)交于点A(1,m),B(n,2).
直线y=-2x+8和双曲线y=$\frac{k}{x}$(k≠0)交于点A(1,m),B(n,2).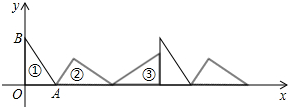 如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).
如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).