题目内容
20. 如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
分析 先由三角函数求出BD,再根据勾股定理求出BC,由?ABCD的面积=BC•BD,即可得出结果即可.
解答 解:∵BD⊥BC,
∴∠DBC=90°,
∵CD=4,sinC=$\frac{3}{4}$,
∴BD=CD•sinC=4×$\frac{3}{4}$=3,
∴AD=$\sqrt{C{D}^{2}-B{C}^{\;}}$=$\sqrt{7}$,
∴?ABCD的面积=BC•BD=3$\sqrt{7}$,
故答案为:$3\sqrt{7}$.
点评 本题考查了平行四边形的性质、三角函数、勾股定理以及平行四边形面积的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,△ABC内接于⊙O,∠ACB=20°,则∠BAO=70度.
如图,△ABC内接于⊙O,∠ACB=20°,则∠BAO=70度.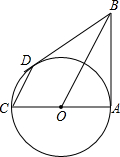 如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.
如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD. 如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.
如图,直线y=x,点A1坐标为(1,0),过点A1作x轴的垂线交直线y=x于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线y=x于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按照此做法进行下去,点B4的纵坐标为2$\sqrt{2}$.