题目内容
2．
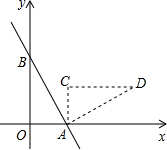如图，一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转90°后得到△ACD，则点D的坐标是（7，3）．
分析 先根据坐标轴上点的坐标特征求出A点和B点坐标，得到OA和OB的长，再根据旋转的性质得到∠CAO=90°，∠ACD=∠AOB=90°，AC=AO=3，CD=OB=4，则CD∥x轴，然后根据第一象限点的坐标特征写出D点坐标．
解答 解：当x=0时，y=-$\frac{4}{3}$x+4=4，则B（0，4），
当y=0时，-$\frac{4}{3}$x+4=0，解得x=3，则A（3，0），
∵△AOB绕点A顺时针旋转90°后得到△ACD，
∴∠CAO=90°，∠ACD=∠AOB=90°，AC=AO=3，CD=OB=4，
∴CD∥x轴，
∴D点坐标为（7，3）．
故答案（7，3）．
点评 本题考查了坐标与图形变换：旋转图形的坐标：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．也考查了一次函数图象上点的坐标特征．
练习册系列答案
相关题目
12．
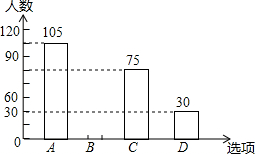某中学在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如下两种不完整的统计图表：
结合上述统计图表，回答下列问题：
（1）本次抽查的学生共300人，x=30%，并将条形统计图补充完整；
（2）如果该校学生有2000人，请估计该校喜爱“篮球”这项球类运动的学生约有多少人？
（3）学校决定举行一次乒乓球比赛，甲，乙，丙，丁四人参加比赛，从四人中随机抽取两人打第一场比赛，请用树状图或列表法所抽到的两人恰好是甲和丁的概率．
某中学在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如下两种不完整的统计图表：| 选项 | 球类运动 | 百分比 |
| A | 乒乓球 | 35% |
| B | 羽毛球 | x |
| C | 篮球 | 25% |
| D | 其他 | 10% |
（1）本次抽查的学生共300人，x=30%，并将条形统计图补充完整；
（2）如果该校学生有2000人，请估计该校喜爱“篮球”这项球类运动的学生约有多少人？
（3）学校决定举行一次乒乓球比赛，甲，乙，丙，丁四人参加比赛，从四人中随机抽取两人打第一场比赛，请用树状图或列表法所抽到的两人恰好是甲和丁的概率．
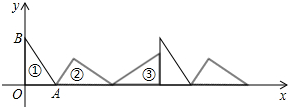如图①，在△AOB中，∠AOB=90°，OA=3，OB=4，将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转，分别得到图②、图③、…，则旋转得到的图⑧的直角顶点的坐标为（$\frac{144}{5}$，$\frac{12}{5}$）．
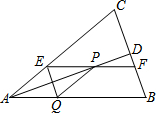如图，等腰三角形ABC中，AB=AC，AD平分∠BAC交BC于点D，在线段AD上任取一点P（点A除外），过点P作EF∥AB，分别交AC，BC于点E和点F，作PQ∥AC，交