题目内容
15.(1)计算2-1-$|{-2\sqrt{3}}|$+($\sqrt{2}$-2)0+$\sqrt{12}$;(2)化简$(\frac{3}{x+1}-x+1)÷\frac{{{x^2}-4x+4}}{x+1}$.
分析 (1)根据负整数指数幂、去绝对值的方法、零指数幂可以解答本题;
(2)先对括号内的式子化简,然后能分解因式的先分解因式,然后化简即可解答本题.
解答 解:(1)2-1-$|{-2\sqrt{3}}|$+($\sqrt{2}$-2)0+$\sqrt{12}$
=$\frac{1}{2}-2\sqrt{3}+1+2\sqrt{3}$
=$\frac{3}{2}$;
(2)$(\frac{3}{x+1}-x+1)÷\frac{{{x^2}-4x+4}}{x+1}$
=$\frac{3-(x-1)(x+1)}{x+1}×\frac{x+1}{(x-2)^{2}}$
=$\frac{3-{x}^{2}+1}{x+1}×\frac{x+1}{(x-2)^{2}}$
=$\frac{(2+x)(2-x)}{x+1}×\frac{x+1}{(x-2)^{2}}$
=$\frac{2+x}{2-x}$.
点评 本题考查分式的混合运算、实数的运算、零指数幂、负整数指数幂、因式分解,解题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目

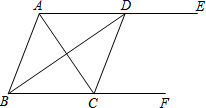 如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.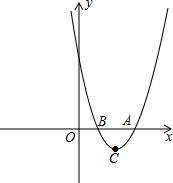 如图,在平面直角坐标系中,抛物线y=x2-4x+3的顶点为C,与x轴交于A、B两点.
如图,在平面直角坐标系中,抛物线y=x2-4x+3的顶点为C,与x轴交于A、B两点.