题目内容
20.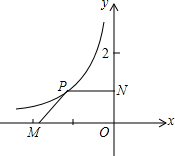 如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )
如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )| A. | 逐渐增大 | B. | 始终不变 | C. | 逐渐减小 | D. | 先增后减 |
分析 由双曲线y=-$\frac{1}{x}$(x<0)设出点P的坐标,运用坐标表示出四边形ONPM的面积函数关系式即可判定.
解答 解:设点P的坐标为(x,-$\frac{1}{x}$),
∵PN⊥y轴于点N,点M是x轴负半轴上的一个定点,
∴四边形OAPB是个直角梯形,
∴四边形ONPM的面积=$\frac{1}{2}$(PN+MO)•NO=$\frac{1}{2}$(-x+MO)•-$\frac{1}{x}$=$\frac{1}{2}-\frac{1}{2x}×OM$,
∵MO是定值,
∴四边形ONPM的面积是个增函数,即点P的横坐标逐渐增大时四边形ONPM的面积逐渐增大.
故选A.
点评 本题主要考查了反比例函数系数k的几何意义,解题的关键是运用点的坐标求出四边形OAPB的面积的函数关系式.

练习册系列答案
相关题目
11.如果∠1与∠2的两边互相平行,那么这两个角( )
| A. | 相等 | B. | 互补 | C. | 相等或互补 | D. | 无法确定 |
12.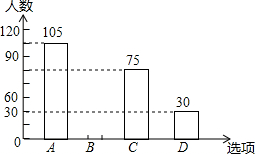 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
结合上述统计图表,回答下列问题:
(1)本次抽查的学生共300人,x=30%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请估计该校喜爱“篮球”这项球类运动的学生约有多少人?
(3)学校决定举行一次乒乓球比赛,甲,乙,丙,丁四人参加比赛,从四人中随机抽取两人打第一场比赛,请用树状图或列表法所抽到的两人恰好是甲和丁的概率.
 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:| 选项 | 球类运动 | 百分比 |
| A | 乒乓球 | 35% |
| B | 羽毛球 | x |
| C | 篮球 | 25% |
| D | 其他 | 10% |
(1)本次抽查的学生共300人,x=30%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请估计该校喜爱“篮球”这项球类运动的学生约有多少人?
(3)学校决定举行一次乒乓球比赛,甲,乙,丙,丁四人参加比赛,从四人中随机抽取两人打第一场比赛,请用树状图或列表法所抽到的两人恰好是甲和丁的概率.
 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分面积为4-π.
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=4,以点A为圆心,AC长为半径作弧,交AB于点D,则图中阴影部分面积为4-π.
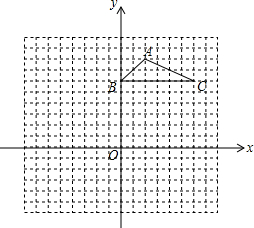 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系. 如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.
如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.