题目内容
5．
仅用无刻度的直尺，按要求画图（保留画图痕迹，不写作法）（1）如图①，画出⊙O的一个内接矩形；
（2）如图②，AB是⊙O的直径，CD是弦，且AB∥CD，画出⊙O的内接正方形．
分析 （1）根据对角线相等且互相平分的四边形是矩形，画出圆的两条直径，即可得到⊙O的一个内接矩形；
（2）根据对角线相等且互相垂直平分的四边形是正方形，画出圆的一条直径，使其与AB互相垂直，即可得到⊙O的内接正方形．
解答 解：（1）如图所示，过O作⊙O的直径AC与BD，连接AB，BC，CD，DA，则四边形ABCD即为所求；
（2）如图所示，延长AC，BD交于点E，连接AD，BC交于点F，连接EF并延长交⊙O于G，H，连接AH，HB，BG，GA，则四边形AHBG即为所求．
点评 本题主要考查了复杂作图以及圆的性质的运用，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
2．
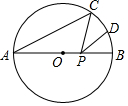如图，在半径为1的⊙O中，∠BAC=30°，点D是劣弧CB的中点，点P是直径AB上的一个动点，则CP+DP的最小值为（ ）
如图，在半径为1的⊙O中，∠BAC=30°，点D是劣弧CB的中点，点P是直径AB上的一个动点，则CP+DP的最小值为（ ）| A． | $\sqrt{2}$ | B． | $\frac{{2\sqrt{2}}}{3}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}-1$ |
如图，?ABCD的对角线AC，BD相交于点O，且AB=5，AC=8，BD=6，求证：?ABCD是菱形．
20．
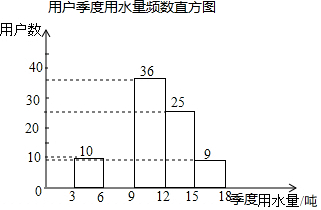某社区为了进一步提高居民珍惜谁、保护水和水忧患意识，提倡节约用水，从本社区5000户家庭中随机抽取100户，调查他们家庭每季度的平均用水量，并将调查的结果绘制成如下的两幅不完整的统计图和表：
用户季度用水量频数分布表
请根据上面的统计图表，解答下列问题：
（1）在频数分布表中：m=20，n=0.25；
（2）根据题中数据补全频数直方图；
（3）如果自来水公司将基本季度水量定为每户每季度9吨，不超过基本季度用水量的部分享受基本价格，超出基本季度用水量的部分实行加价收费，那么该社区用户中约有多少户家庭能够全部享受基本价格？
某社区为了进一步提高居民珍惜谁、保护水和水忧患意识，提倡节约用水，从本社区5000户家庭中随机抽取100户，调查他们家庭每季度的平均用水量，并将调查的结果绘制成如下的两幅不完整的统计图和表：用户季度用水量频数分布表
| 平均用水量（吨） | 频数 | 频率 |
| 3＜x≤6 | 10 | 0.1 |
| 6＜x≤9 | m | 0.2 |
| 9＜x≤12 | 36 | 0.36 |
| 12＜x≤15 | 25 | n |
| 15＜x≤18 | 9 | 0.09 |
（1）在频数分布表中：m=20，n=0.25；
（2）根据题中数据补全频数直方图；
（3）如果自来水公司将基本季度水量定为每户每季度9吨，不超过基本季度用水量的部分享受基本价格，超出基本季度用水量的部分实行加价收费，那么该社区用户中约有多少户家庭能够全部享受基本价格？
10．下列计算正确的是（ ）
| A． | $\sqrt{3}$+$\sqrt{6}$=3 | B． | $\sqrt{2}$×$\sqrt{6}$=3$\sqrt{2}$ | C． | $\sqrt{8}$÷$\sqrt{2}$=4 | D． | （$\sqrt{12}$-$\sqrt{3}$）×$\sqrt{3}$=3 |
如图，在四边形ABCD中，已知AB∥DC，AB=DC，在不添加任何辅助线的情况下，请补充一个条件，使四边形ABCD成为矩形，这个条件是∠A=90°．
14．下列关于x的方程中，是分式方程的是（ ）
| A． | 3x=$\frac{1}{2}$ | B． | $\frac{x+2}{5}$=$\frac{3+x}{4}$ | C． | $\frac{1}{x}$=2 | D． | 3x-2y=1 |
15．下列各式是完全平方式的是（ ）
| A． | x2+2x-1 | B． | 1+x2 | C． | x+xy+1 | D． | ${x^2}-x+\frac{1}{4}$ |