题目内容
13. 如图,?ABCD的对角线AC,BD相交于点O,且AB=5,AC=8,BD=6,求证:?ABCD是菱形.
如图,?ABCD的对角线AC,BD相交于点O,且AB=5,AC=8,BD=6,求证:?ABCD是菱形.
分析 首先由勾股定理的逆定理证明△AOB为直角三角形,从而得到AC⊥BD,然后根据对角线相互垂直的平行四边形是菱形判定即可.
解答 证明:∵四边形ABCD是平行四边形,且AC=8,BD=6,
∴AO=4,BO=3,
∵AB=5,
∴AB2=AO2+BO2.
∴△OAB是直角三角形.
∴AC⊥BD.
又∵四边形ABCD为平行四边形,
∴四边形ABCD为菱形.
点评 本题主要考查的是菱形的判定、平行四边形的性质等知识,掌握勾股定理的逆定理的应用、菱形的判定是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
4. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB、EC、DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB、EC、DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB、EC、DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB、EC、DB,添加一个条件,不能使四边形DBCE成为矩形的是( )| A. | AB=BE | B. | BE⊥DC | C. | ∠ADB=90° | D. | CE⊥DE |
1.下列x的值不是不等式-2x+4<0的解,答案是( )
| A. | -2 | B. | 3 | C. | 3.5 | D. | 10 |
 如图,△ABC中,AB=AC,AD、AE分别是∠BAC和外角∠BAF的平分线,且BE⊥AE.
如图,△ABC中,AB=AC,AD、AE分别是∠BAC和外角∠BAF的平分线,且BE⊥AE.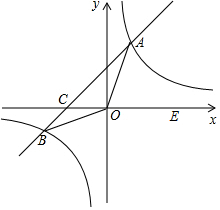 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$. 如图,点P是菱形ABCD对角线AC上一个动点,PE⊥AD,PF⊥CD.
如图,点P是菱形ABCD对角线AC上一个动点,PE⊥AD,PF⊥CD. 仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)
仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法) 如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是2≤x≤5.
如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是2≤x≤5. 已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且∠AQP=90°.
已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且∠AQP=90°.