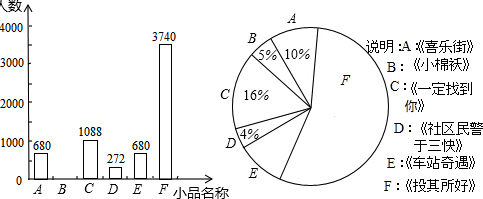
题目内容
6. 如图,为测量某楼AB的高度,工作人员在点D处高1.8m的测角仪CD测得楼顶端A的仰角为30°,向前走40m到点E,又测得点A的仰角为60°,求楼AB的高度.(最后结果取近似值,保留两位小数,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,为测量某楼AB的高度,工作人员在点D处高1.8m的测角仪CD测得楼顶端A的仰角为30°,向前走40m到点E,又测得点A的仰角为60°,求楼AB的高度.(最后结果取近似值,保留两位小数,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 首先由题意易得△ACF是等腰三角形,继而求得AF的长,然后在Rt△AFG中,利用三角函数的知识求得AG的长,继而求得答案.
解答 解:∵∠ACG=30°,∠AFG=60°,
∴∠CAF∠AFG-∠ACG=30°,
∴∠ACF=∠CAF,
∴AF=CF=DF=40m,
∴AG=AF•sin60°=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$=20×1.732=34.64(m),
∵BG=1.8m,
∴AB=(34.64+1.8)=36.44(m).
答:楼AB的高度为6.44m.
点评 本题考查仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.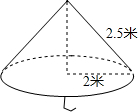 一把大遮阳伞伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则伞面的面积是( )
一把大遮阳伞伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则伞面的面积是( )
 一把大遮阳伞伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则伞面的面积是( )
一把大遮阳伞伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则伞面的面积是( )| A. | $\frac{25}{4}$平方米 | B. | 5π平方米 | C. | 10π平方米 | D. | $\frac{15}{4}$π平方米 |
1.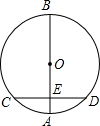 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
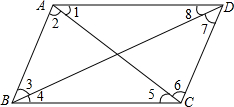 如图,在图中标示的角∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8中,内错角有几对,它们分别是哪两条直线被哪两条直线所截而构成的?
如图,在图中标示的角∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8中,内错角有几对,它们分别是哪两条直线被哪两条直线所截而构成的?