Question

1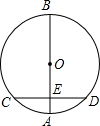．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，那么线段OE的长为（　　）

• A． 10
• B． 8
• C． 6
• D． 4

Answer 1

分析 连接OD，由直径AB与弦CD垂直，根据垂径定理得到E为CD的中点，由CD的长求出DE的长，又由直径的长求出半径OD的长，在直角三角形ODE中，由DE及OD的长，利用勾股定理即可求出OE的长．

解答 解：如图所示，连接OD．
∵弦CD⊥AB，AB为圆O的直径，
∴E为CD的中点，
又∵CD=16，
∴CE=DE=$\frac{1}{2}$CD=8，
又∵OD=$\frac{1}{2}$AB=10，
∵CD⊥AB，
∴∠OED=90°，
在Rt△ODE中，DE=8，OD=10，
根据勾股定理得：OE²+DE²=OD²，
∴OE=$\sqrt{O{D}^{2}-D{E}^{2}}$=6，
则OE的长度为6，
故选C．

点评 本题主要考查了垂径定理，勾股定理，解答此类题常常利用垂径定理由垂直得中点，进而由弦长的一半，弦心距及圆的半径构造直角三角形，利用勾股定理是解答此题的关键．