题目内容
9.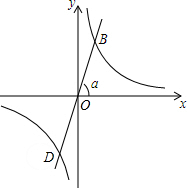 如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.
如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.(1)若已知点A(-m,0),C(m,0),不论m取何值,四边形ABCD的形状一定是平行四边形;
(2)若已知点A(-m,0),C(m,0),当点B为(P,1)时,四边形ABCD是矩形,则P=$\sqrt{3}$,m=2;
(3)若点P的坐标为(P,1)时,要使四边形ABCD是菱形,则AC所在直线解析式为y=-$\sqrt{3}$x.
分析 (1)由正比例函数与反比例函数均关于原点对称,可得OB=OD,又由OA=OC,根据对角线互相平分的四边形是平行四边形,即可判定四边形ABCD的形状一定是平行四边形;
(2)由点B为(p,1),代入反比例函数y=$\frac{\sqrt{3}}{x}$,即可求得p的值;然后由当AC=BD时,即OB=OD=OA=OC时,?ABCD是矩形,求得m的值;
(3)由点B为(p,1),可求得α的值,继而求得A、C所在直线与y轴的夹角,继而求得直线AC上点的坐标,则可求得答案.
解答 解:(1)∵正比例函数与反比例函数均关于原点对称,
∴点B与点D关于原点对称,
∴OB=OD,
∵点A(-m,0),C(m,0),
∴OA=OC,
∴四边形ABCD的形状一定是平行四边形;
(2)∵点B为(p,1),
∴1=$\frac{\sqrt{3}}{p}$,
解得:p=$\sqrt{3}$;
∴OB=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∵当AC=BD时,即OB=OD=OA=OC时,?ABCD是矩形,
∴m=2;
(3)过点B作BE⊥x轴于点E,
∵点B为(p,1),
∴点B的坐标为:($\sqrt{3}$,1),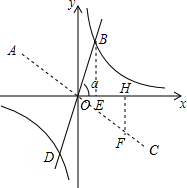
∴tanα=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴α=30°,
∵当AC⊥BD时,?ABCD是菱形,
设点F在直线AC上,过点F作FH⊥x轴于点H,
∴∠FOH=60°,
设点F的坐标为:(1,-$\sqrt{3}$),
设直线AC的解析式为:y=kx,
则-$\sqrt{3}$=k,
∴直线AC的解析式为:y=-$\sqrt{3}$x.
故答案为:(1)平行四边形,(2)$\sqrt{3}$,2,(3)y=-$\sqrt{3}$x.
点评 此题属于反比例函数综合题,考查了待定系数求函数解析式的知识、点与函数图象的关系、平行四边形的判定与性质、矩形与菱形的判定.注意第三问中,求得直线AC上一点的坐标是关键.

 名校课堂系列答案
名校课堂系列答案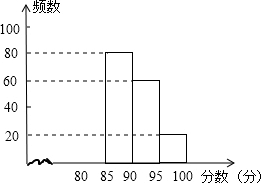 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
(1)求出表中a、b、c的数值,并补全频数分布直方图;
(2)如果成绩在95分以上(含95分)的可以获得特等奖,那么获奖的同学获得特等奖的概率是多少?
(3)获奖成绩的中位数落在哪个分数段?并估算全部获奖同学的平均分.
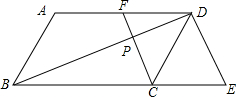 如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连结DE、CF,连接BD交CF于点P.
如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连结DE、CF,连接BD交CF于点P.