题目内容
19.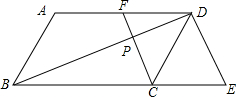 如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连结DE、CF,连接BD交CF于点P.
如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连结DE、CF,连接BD交CF于点P.(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠ABC=60°,求△DCE的周长;
(3)在(2)的条件下,求△BPC的面积.
分析 (1)根据平行四边形的性质得到AD∥BC 且 AD=BC,根据三角形的中位线的性质得到DF=$\frac{1}{2}$AD,又∵CE=$\frac{1}{2}$BC,得到DF∥EC,DF=EC,于是推出四边形CEDF为平行四边形;
(2)过D作DH⊥BE于H,根据平行四边形的性质得到∠DCE=60°,求出CD=4,CH=2,DH=2$\sqrt{3}$,由勾股定理得到DE=$\sqrt{13}$,于是求得结果;
(3)过P作PM⊥BC于M,由于PC∥DE,得到△PBC∽△DBE,根据相似三角形的性质得到$\frac{PM}{DH}=\frac{BC}{BE}=\frac{2}{3}$,求得DH=2$\sqrt{3}$,根据三角形的面积公式即可得到结论.
解答 解:(1)在平行四边形ABCD中,
∵AD∥BC 且 AD=BC,
∵F为AC中点,
∴DF=$\frac{1}{2}$AD,又∵CE=$\frac{1}{2}$BC,
∴DF∥EC,DF=EC
∴四边形CEDF为平行四边形;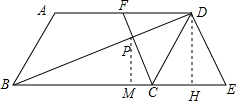
(2)过D作DH⊥BE于H,
在平行四边形ABCD中,
∵∠ABC=60°,
∴∠DCE=60°,
∵AB=4,
∴CD=4,
∴CH=2,DH=2$\sqrt{3}$,
在平行四边形CEDF中,CE=DF=$\frac{1}{2}$AD=3,
∴EH=1,
∴DE=$\sqrt{13}$,
∴△DCE的周长=7+$\sqrt{13}$;
(3)过P作PM⊥BC于M,
∵PC∥DE,
∴△PBC∽△DBE,
∴$\frac{PM}{DH}=\frac{BC}{BE}=\frac{2}{3}$,
∵DH=2$\sqrt{3}$,
∴PM=$\frac{4\sqrt{3}}{3}$,
∴S△BPC=4$\sqrt{3}$.
点评 本题考查了平行四边形的判定和性质,相似三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,在矩形ABCD中,AB=6,BC=8,E,G分别在AD,CD上,沿BE,BG折叠矩形,点A和点C分别落在BD上的点F,H处.
如图,在矩形ABCD中,AB=6,BC=8,E,G分别在AD,CD上,沿BE,BG折叠矩形,点A和点C分别落在BD上的点F,H处.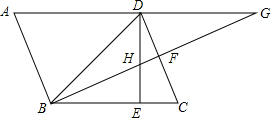 如图,BD是平行四边形ABCD的对角线,若∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE与BF相交于H,BF与AD的延长线相交于G.求证:
如图,BD是平行四边形ABCD的对角线,若∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE与BF相交于H,BF与AD的延长线相交于G.求证: 如图,已知在等腰△ABC中,∠A=∠B=30°.
如图,已知在等腰△ABC中,∠A=∠B=30°.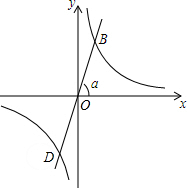 如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.
如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.