题目内容
14.计算:(1)6xy$•\frac{{y}^{2}}{15{x}^{2}}$;
(2)$\frac{-4xy}{9x{y}^{3}}÷\frac{1}{3{x}^{2}}$;
(3)$\frac{1}{x}÷\frac{1}{x-{x}^{2}}$;
(4)(a2-ab)$÷\frac{b-a}{ab}$;
(5)$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}+4x+4}$•$\frac{x+2}{3{x}^{2}+6xy}$.
分析 (1)约分即可;
(2)除法转化为乘法,约分;
(3)因式分解后除法转化为乘法,约分;
(4)先将被除式因式分解,再将除法转化为乘法,最后约分;
(5)分子、分母因式分解,约分后计算乘方可得.
解答 解:(1)原式=$\frac{6x{y}^{3}}{15{x}^{2}}$=$\frac{3x•2{y}^{3}}{3x•5x}$=$\frac{2{y}^{3}}{5x}$;
(2)原式=-$\frac{4}{9{y}^{2}}$•3x2=-$\frac{4{x}^{2}}{3{y}^{2}}$;
(3)原式=$\frac{1}{x}$•x(1-x)=1-x;
(4)原式=a(a-b)•$\frac{ab}{-(a-b)}$=-a2b;
(5)原式=$\frac{(x+2y)(x-2y)}{(x+2)^{2}}$•$\frac{x+2}{3x(x+2y)}$
=$\frac{x-2y}{3x(x+2)}$
=$\frac{x-2y}{3{x}^{2}+6x}$.
点评 本题主要考查分式的混合运算,熟练掌握分式混合运算的顺序是解题的根本和关键.

练习册系列答案
相关题目
5.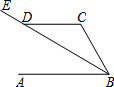 如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )
如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )
 如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )
如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为( )| A. | 150° | B. | 130° | C. | 120° | D. | 100° |
2.在-5,0,π,$\sqrt{2}$这四个数中,最大的有理数的是( )
| A. | -5 | B. | 0 | C. | π | D. | $\sqrt{2}$ |
6.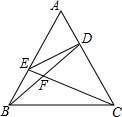 如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为( )
如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为( )
 如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为( )
如图所示,正三角形ABC的边长为2,$\frac{AE}{BE}$=2,$\frac{AD}{DC}$=$\frac{1}{2}$,BD交CE于点F,则△AEF的外接圆半径长为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{7}$ |
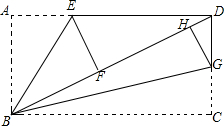 如图,在矩形ABCD中,AB=6,BC=8,E,G分别在AD,CD上,沿BE,BG折叠矩形,点A和点C分别落在BD上的点F,H处.
如图,在矩形ABCD中,AB=6,BC=8,E,G分别在AD,CD上,沿BE,BG折叠矩形,点A和点C分别落在BD上的点F,H处.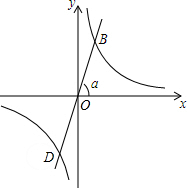 如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.
如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D. 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,求证:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形.
如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,求证:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形.