题目内容
18．若不等式组$\left\{\begin{array}{l}{x≤2}\\{x＞m+1}\end{array}\right.$恰有三个整数解，则m的取值范围是-2≤m＜-1．分析 首先确定不等式组的整数解，然后根据不等式的整数解得到一个关于m的不等式组，从而求解．
解答 解：∵不等式组$\left\{\begin{array}{l}{x≤2}\\{x＞m+1}\end{array}\right.$恰有三个整数解，则整数解为0、1、2，
∴-1≤m+1＜0，
解得：-2≤m＜-1．
故答案为：-2≤m＜-1．
点评 本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
相关题目
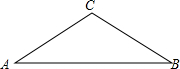如图，已知在等腰△ABC中，∠A=∠B=30°．
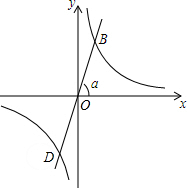如图，正比例函数的图象与x轴正方向所成角为α度，若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D．
13．2tan60°，$\sqrt{8}$，$\root{3}{16}$，π这四个实数中，最大的数是（ ）
| A． | 2tan60° | B． | $\sqrt{8}$ | C． | $\root{3}{16}$ | D． | π |
如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，求证：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形．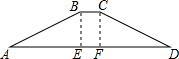
如图，为消除淮河灾害，某市水利部门修建了横断面是梯形的淮河大坝，坝顶宽6米，坝高BE=CF=20米，斜坡AB的坡角∠A=30°，斜坡CD的坡度i=1：3，（坡度是指坡面的铅直高度与水平宽度的比）．求坝底AD的宽．（结果保留整数，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）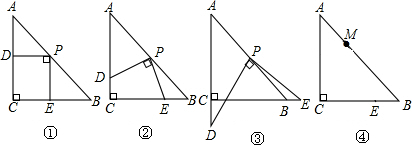
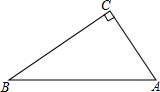如图，已知△ABC中，∠ACB=90°，AC=3，BC=5，M为AB的中点．