题目内容
6.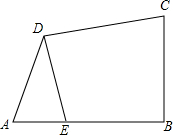 已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.
已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.(1)求证:△ADE是等腰三角形.
(2)若BE+BC=4,求四边形BCDE的面积.
分析 (1)连接AC,根据等腰三角形的性质得出∠DAC=∠DCA,∠BAC=∠BCA,即可得出∠DAB=∠BCD,根据四边形内角和定理得到∠DEB+∠BCD=180°,进而可得出∠AED=∠BCD,即可得出∠DAB=∠AED,根据等腰三角形的判定即可证得结论,
(2)连接CE,根据BE+BC=4,得出(BE+BC)2=16,进一步得出BE2+BC2+2BE•BC=16,然后根据勾股定理和三角形面积公式即可得到4×$\frac{1}{2}$CD2+4×$\frac{1}{2}$BE•BC=16,即可证得S△DCE+S△BEC=4,即四边形BCDE的面积=4.
解答 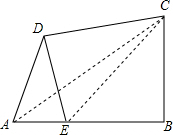 (1)证明:连接AC,
(1)证明:连接AC,
∵AB=BC,AD=CD,
∴∠DAC=∠DCA,∠BAC=∠BCA,
∴∠DAC+∠BAC=∠DCA+∠BCA,
即∠DAB=∠BCD,
∵∠ABC=90°,DE⊥CD,
∴∠DEB+∠BCD=180°,
∵∠AED+∠DEB=180°,
∴∠AED=∠BCD,
∴∠DAB=∠AED,
∴AD=ED,
∴△ADE是等腰三角形;
(2)解:连接CE,
∵BE+BC=4,
∴(BE+BC)2=16,
∴BE2+BC2+2BE•BC=16,
∵BE2+BC2=CE2=CD2+DE2,
∵CD=DE,
∴CE2=2CD2,
∴CE2=4×$\frac{1}{2}$CD2,
∴4×$\frac{1}{2}$CD2+4×$\frac{1}{2}$BE•BC=16,
∴4S△DCE+4S△BEC=16,
∴S△DCE+S△BEC=4,
即四边形BCDE的面积=4.
点评 本题考查了等腰三角形的判定和性质,四边形内角和定理,勾股定理的应用以及三角形面积等,证得∠DAB=∠BCD是解题的关键.

练习册系列答案
相关题目
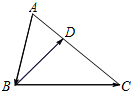 如图,在△ABC中,点D在AC边上且AD:DC=1:2,若$\overrightarrow{AB}=\overrightarrow{m}$,$\overrightarrow{BD}=\overrightarrow{n}$,那么$\overrightarrow{DC}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$(用向量$\overrightarrow{m}$、$\overrightarrow{n}$表示).
如图,在△ABC中,点D在AC边上且AD:DC=1:2,若$\overrightarrow{AB}=\overrightarrow{m}$,$\overrightarrow{BD}=\overrightarrow{n}$,那么$\overrightarrow{DC}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$(用向量$\overrightarrow{m}$、$\overrightarrow{n}$表示).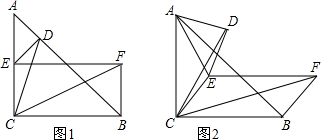
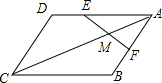 如图,AC是?ABCD的对角线,点E在AD上,AE=2DE,点F是AB的中点,连接EF交AC于点M,若AC=14,则AM=4.
如图,AC是?ABCD的对角线,点E在AD上,AE=2DE,点F是AB的中点,连接EF交AC于点M,若AC=14,则AM=4.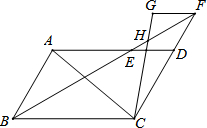 ?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.
?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.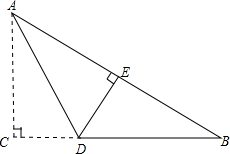 如图,Rt△ABC中,∠C=90°,现将直角边AC折叠到AB边上,点C落在AB边上的E点,折痕为AD,若AC=6,BC=8.求△ADB的面积.
如图,Rt△ABC中,∠C=90°,现将直角边AC折叠到AB边上,点C落在AB边上的E点,折痕为AD,若AC=6,BC=8.求△ADB的面积.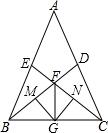 如图,在△ABC中,点E在AB上,点D在AC上,G为BC的中点,BE=CD,∠BEC=∠CDB,BD与CE相交于点F,GM⊥BF,GN⊥CF,垂足分别为M,N.
如图,在△ABC中,点E在AB上,点D在AC上,G为BC的中点,BE=CD,∠BEC=∠CDB,BD与CE相交于点F,GM⊥BF,GN⊥CF,垂足分别为M,N. 如图,在平面直角坐标系中,△AOB是等边三角形,且边长为2,则点A的坐标为A(1,$\sqrt{3}$).
如图,在平面直角坐标系中,△AOB是等边三角形,且边长为2,则点A的坐标为A(1,$\sqrt{3}$). 如图,在平面直角坐标系x0y中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=0C3,OA3=OC4…,则依此规律,点A2015的横坐标为-4×$(\frac{4}{3})^{1006}$.
如图,在平面直角坐标系x0y中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4=…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=0C3,OA3=OC4…,则依此规律,点A2015的横坐标为-4×$(\frac{4}{3})^{1006}$.