题目内容
11.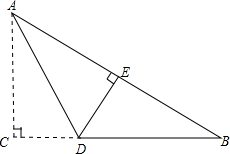 如图,Rt△ABC中,∠C=90°,现将直角边AC折叠到AB边上,点C落在AB边上的E点,折痕为AD,若AC=6,BC=8.求△ADB的面积.
如图,Rt△ABC中,∠C=90°,现将直角边AC折叠到AB边上,点C落在AB边上的E点,折痕为AD,若AC=6,BC=8.求△ADB的面积.
分析 根据翻折不变性得到AC=AE=6,设CD=DE=x,在RT△DEB中利用勾股定理即可解决.
解答 解; 在RT△ABC中,∵∠C=90°,AC=6,BC=8,
在RT△ABC中,∵∠C=90°,AC=6,BC=8,
∵AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵△ADE是由△ADC翻折得到,
∴AE=AC=6,CD=DE,∠C=∠AED=∠DEB=90°,设CD=DE=x,
∴在RT△DEB中,∵∠DEB=90°,EB=AB-AE=4,DE=x,DB=8-x,
∴(8-x)2=x2+42,
∴x=3,
∴DE=3,
∴S△ADB=$\frac{1}{2}$•AB•DE=$\frac{1}{2}$×10×3=15.
点评 本题考查翻折变换、勾股定理等知识,解题的关键是利用翻折不变性得到CD=DE,AC=AE,学会转化的思想,把问题转化为方程,用方程的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
2. 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
1.下列各图中,能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
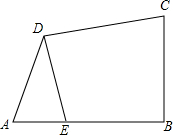 已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.
已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.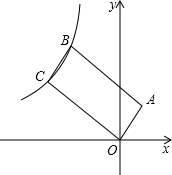 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.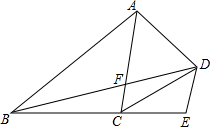 四边形ABCD中,AD=CD,∠ADB=∠ACB,DE∥AC,交BC延于E,求证:AD2=AF•DE.
四边形ABCD中,AD=CD,∠ADB=∠ACB,DE∥AC,交BC延于E,求证:AD2=AF•DE.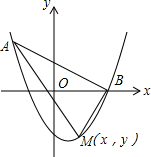 如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.
如图,点A(-2,5)在以(1,-4)为顶点的抛物线上,抛物线与x正半轴交于点B,点M(x,y)(其中-2<x<3)是抛物线上的动点,则△ABM面积的最大值为$\frac{125}{8}$.