题目内容
15.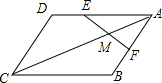 如图,AC是?ABCD的对角线,点E在AD上,AE=2DE,点F是AB的中点,连接EF交AC于点M,若AC=14,则AM=4.
如图,AC是?ABCD的对角线,点E在AD上,AE=2DE,点F是AB的中点,连接EF交AC于点M,若AC=14,则AM=4.
分析 根据四边形ABCD是平行四边形,得到AO=CO=$\frac{1}{2}$AC=7,AD∥BC,AD=BC,根据三角形的中位线的性质得到OF∥BC,OF=$\frac{1}{2}$BC,得到$\frac{AE}{OF}$=$\frac{4}{3}$,根据相似三角形的性质即可得到结论.
解答 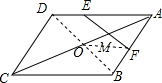 解:连接BD交AC于O,连接OF,
解:连接BD交AC于O,连接OF,
∵四边形ABCD是平行四边形,
∴AO=CO=$\frac{1}{2}$AC=7,AD∥BC,AD=BC,
∵点F是AB的中点,
∴OF∥BC,OF=$\frac{1}{2}$BC,
∴OF∥AD,OF=$\frac{1}{2}$AD,
∵AE=2DE,
∴AE=$\frac{2}{3}$AD,
∴$\frac{AE}{OF}$=$\frac{4}{3}$,
∵OF∥AE,
∴△AEM∽△OMF,
∴$\frac{AM}{OM}=\frac{AE}{OF}$=$\frac{4}{3}$,
∴AM=4.
故答案为:4.
点评 题主要考查了平行四边形的性质以及相似三角形的判定与性质,得出△AEM∽△OFM是解题关键.

练习册系列答案
相关题目
6.①对顶角相等;②两点之间线段最短;③相等的角是对顶角;④同位角相等.其中假命题有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
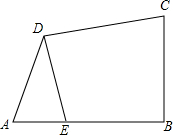 已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.
已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.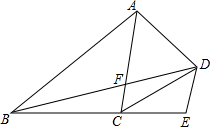 四边形ABCD中,AD=CD,∠ADB=∠ACB,DE∥AC,交BC延于E,求证:AD2=AF•DE.
四边形ABCD中,AD=CD,∠ADB=∠ACB,DE∥AC,交BC延于E,求证:AD2=AF•DE.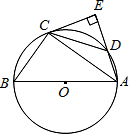 如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.