题目内容
17.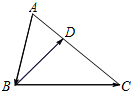 如图,在△ABC中,点D在AC边上且AD:DC=1:2,若$\overrightarrow{AB}=\overrightarrow{m}$,$\overrightarrow{BD}=\overrightarrow{n}$,那么$\overrightarrow{DC}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$(用向量$\overrightarrow{m}$、$\overrightarrow{n}$表示).
如图,在△ABC中,点D在AC边上且AD:DC=1:2,若$\overrightarrow{AB}=\overrightarrow{m}$,$\overrightarrow{BD}=\overrightarrow{n}$,那么$\overrightarrow{DC}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$(用向量$\overrightarrow{m}$、$\overrightarrow{n}$表示).
分析 由$\overrightarrow{AB}=\overrightarrow{m}$,$\overrightarrow{BD}=\overrightarrow{n}$,直接利用三角形法则求解,即可求得$\overrightarrow{AD}$,又由点D在AC边上且AD:DC=1:2,即可求得答案.
解答 解:∵$\overrightarrow{AB}=\overrightarrow{m}$,$\overrightarrow{BD}=\overrightarrow{n}$,
∴$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{m}$+$\overrightarrow{n}$,
∵点D在AC边上且AD:DC=1:2,
∴$\overrightarrow{DC}$=2$\overrightarrow{AD}$=2$\overrightarrow{m}$+2$\overrightarrow{n}$.
故答案为:2$\overrightarrow{m}$+2$\overrightarrow{n}$.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用是解此题的关键.

练习册系列答案
相关题目
2. 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
 如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
如图,平行四边形ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
6.①对顶角相等;②两点之间线段最短;③相等的角是对顶角;④同位角相等.其中假命题有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
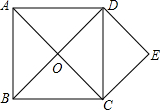 如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作CE∥BD,DE∥AC.求证:四边形OCED是正方形.
如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作CE∥BD,DE∥AC.求证:四边形OCED是正方形.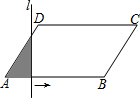 如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.
如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.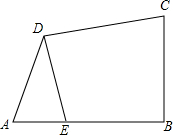 已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.
已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.