题目内容
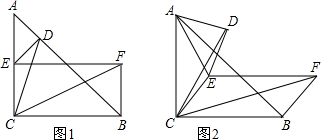
18.在△ABC中,∠ACB=90°,AC=BC,以BC为边作?BCEF,以AE为斜边在同一侧作等腰直角三角形ADE,连接CD、CF.(1)如图1,若?BCEF为矩形,则CF与CD的数量关系是CF=$\sqrt{2}$CD;
(2)如图2,探究CF与CD的数量关系,并证明.
分析 (1)如图1中,结论:CF=$\sqrt{2}$CD,作DM⊥AC,DN⊥EF垂足分别为M、N,连接DF,只要证明△DMC≌△DNF即可.
(2)如图2中,结论:CF=$\sqrt{2}$CD.作DM⊥AC,DN⊥EF垂足分别为M、N,连接DF,延长FE交AC于H,先证明△ADM≌△EDN再证明△DMC≌△DNF即可.
解答 解:(1)如图1中,结论:CF=$\sqrt{2}$CD.
理由: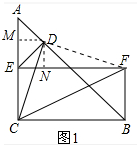 作DM⊥AC,DN⊥EF垂足分别为M、N,连接DF.
作DM⊥AC,DN⊥EF垂足分别为M、N,连接DF.
∵AD=DE,∠ADE=90°,DM⊥AE,
∴AM=ME,
∴DM=AM=ME,
∵∠DME=∠MEN=∠DNE=90°,
∴四边形DMEN是矩形,
∵MD=ME,
∴四边形DMEN是正方形,
∴DM=DN=AM,∠MDN=90°,
∵AC=BC=EF,
∴CM=NF,
在△DMC和△DNF中,
$\left\{\begin{array}{l}{DM=DN}\\{∠DMC=∠DNF=90°}\\{CM=NF}\end{array}\right.$,
∴△DMC≌△DNF,
∴CD=DF,∠CDM=∠FDN,
∴∠CDF=∠MDN=90°,
∴△CDF是等腰直角三角形,
∴CF=$\sqrt{2}$CD.
故答案为CF=$\sqrt{2}$CD.
(2))如图2中,结论:CF=$\sqrt{2}$CD.
理由:作DM⊥AC,DN⊥EF垂足分别为M、N,连接DF,延长FE交AC于H.
∵四边形BCEF是平行四边形,
∴BC=EF=AC,EF∥BC,
∴∠AHF=∠ACB=90°,
∵∠DMH=∠MHN=∠DNH=90°,
∴四边形DMHN是矩形,
∴∠MDN=90°,
∵∠ADE=∠MDN=90°,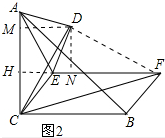
∴∠ADM=∠EDN,
在△ADM和△EDN中,
$\left\{\begin{array}{l}{∠AMD=∠DNE}\\{∠ADM=∠EDN}\\{AD=DE}\end{array}\right.$,
∴△ADM≌△EDN,
∴AM=EN,DM=DN,
∴CM=FN,
在△DMC和△DNF中,
$\left\{\begin{array}{l}{DM=DN}\\{∠DMC=∠DNF=90°}\\{CM=NF}\end{array}\right.$,
∴△DMC≌△DNF,
∴CD=DF,∠CDM=∠FDN,
∴∠CDF=∠MDN=90°,
∴△CDF是等腰直角三角形,
∴CF=$\sqrt{2}$CD.
点评 本题考查平行四边形的性质、矩形的性质、正方形的判定和性质、全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是添加辅助线构造全等三角形,学会常用辅助线的添加方法,属于中考常考题型.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
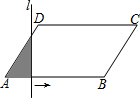 如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.
如图,?ABCD中,AD=6,∠A=60°,AB=10,直线l⊥AB,且从点A开始向右匀速平行移动,每秒运动1个单位长度,设直线l扫过?ABCD的面积(阴影部分)为y,移动的时间为x秒,则当3≤x<10时,y与x的函数关系式是y=$\frac{3\sqrt{3}}{2}$x2-$\frac{9\sqrt{3}}{2}$x.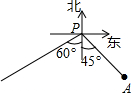 如图,小岛A在港口P的南偏东45°方向、距离港口81海里处.甲船从A出发,沿AP方向以9海里/h的速度驶向港口;乙船从港口P出发,沿南偏西60°方向,以18海里/h的速度驶离港口.现两船同时出发,当甲船在乙船的正东方向时,行驶的时间为9($\sqrt{2}$-1)h.(结果保留根号)
如图,小岛A在港口P的南偏东45°方向、距离港口81海里处.甲船从A出发,沿AP方向以9海里/h的速度驶向港口;乙船从港口P出发,沿南偏西60°方向,以18海里/h的速度驶离港口.现两船同时出发,当甲船在乙船的正东方向时,行驶的时间为9($\sqrt{2}$-1)h.(结果保留根号)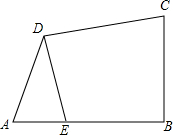 已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.
已知如图,在四边形ABCD中,∠ABC=90°,AB=BC,AD=CD,DE⊥CD交AB于E.