题目内容
5.在矩形ABCD中,E为线段BC上一点,点B关于AE的对称点为F,连接AF,G为BC延长线上一点,且DG=DA,射线EF交射线GD于点P.(1)如图1,当点P在线段GD上时,求证:PF=CG+DP;
(2)如图2,当点P在线段GD的延长线上时,直接写出线段PF、CG、DP之间的数量关系.

分析 (1)如图1中,连接AF,在射线FP上截取FM=CG,连接AM、DM,先证明△AFM≌△DCG,再证明PD=PM即可.
(2)结论:PF=CG-PD.如图2中,连接AF,在射线FP上截取FM=CG,连接AM、DM,先证明△AFM≌△DCG,再证明PD=PM即可.
解答 (1)证明:如图1中,连接AF,在射线FP上截取FM=CG,连接AM、DM.
∵四边形ABCD是矩形,
∴AB=CD,∠B=∠BCD=∠DCG=90°,AD∥BC,
∵B、E关于AE对称,
∴AB=AF,∠B=∠AFE=∠AFM=90°,
∴∠AFM=∠DCG=90°,AF=DC,
在△AFM和△DCG中,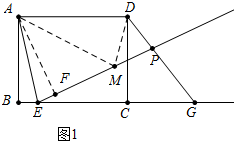
$\left\{\begin{array}{l}{AF=DC}\\{∠AFM=∠DCG}\\{FM=CG}\end{array}\right.$,
∴△AFM≌△DCG,
∴∠DGC=∠AMF,AM=DG=AD,
∴∠ADM=∠AMD,
∵AD∥BG,
∴∠ADG+∠DGC=180°,
∵∠AMF+∠AMP=180°,
∴∠ADG=∠AMP,
∴∠PDM=∠PMD,
∴PD=PM,
∴PF=FM+PM=CG+PD.
(2)结论:PF=CG-PD.
证明:如图2中,连接AF,在射线FP上截取FM=CG,连接AM、DM.
∵四边形ABCD是矩形,
∴AB=CD,∠B=∠BCD=∠DCG=90°,AD∥BC,
∵B、E关于AE对称,
∴AB=AF,∠B=∠AFE=∠AFM=90°,
∴∠AFM=∠DCG=90°,AF=DC,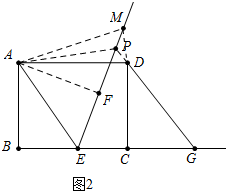
在△AFM和△DCG中,
$\left\{\begin{array}{l}{AF=DC}\\{∠AFM=∠DCG}\\{FM=CG}\end{array}\right.$,
∴△AFM≌△DCG,
∴∠DGC=∠AMF,AM=DG=AD,
∴∠ADM=∠AMD,
∵∠ADP+∠CDG=90°,∠CDG+∠CGD=90°,
∴∠ADP=∠DGC=∠AMP,
∴∠PDM=∠PMD,
∴PD=PM,
∴PF=FM-PM=CG-PD.
点评 本题考查矩形的性质、全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是添加辅助线,构造全等三角形,学会添加辅助线的方法截长补短法,属于中考常考题型.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )| A. | 2 | B. | 3 | C. | $\frac{10}{3}$ | D. | $\frac{13}{3}$ |
 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则线段ON的长为1.
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则线段ON的长为1.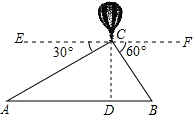 如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?
如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少? 如图,其中邻补角共有3对.
如图,其中邻补角共有3对.