题目内容
15.已知关于x的方程x2-(k+1)x-6=0.(1)求证:无论k的取何实数,该方程总有两个不相等的实数根;
(2)若方程的一根为2,试求出k的值和另一根.
分析 (1)代入数据求出b2-4ac的值,由b2-4ac≥24可证出结论;
(2)将x=2代入到原方程中得到关于k的一元一次方程,解方程可得出k值,将k值代入到原方程,解方程即可得出方程的另外一根.
解答 (1)证明:∵b2-4ac=[-(k+1)]2-4×1×(-6)=(k+1)2+24≥24,
∴无论k的取何实数,该方程总有两个不相等的实数根.
(2)解:将x=2代入方程x2-(k+1)x-6=0中,
22-2(k+1)-6=0,即k+2=0,
解得:k=-2.
∴原方程=x2+x-6=(x-2)(x+3)=0,
解得:x1=2,x2=-3.
故k的值为-2,方程的另一根为-3.
点评 本题考查了根的判别式、解一元一次方程以及解一元二次方程,解题的关键是:(1)计算出b2-4ac≥24;(2)代入x=2求出k值.问题属于基础题,难度不大,解决该题型题目时,由根的判别式的值来判断根的个数是关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
20.已知y是x的一次函数,其部分对应值如下表:
(1)求这个一次函数的表达式,并补全表格;
(2)已知点A(-2,-2)既在这个一次函数图象上,也在反比例函数y=$\frac{m}{x}$图象上,求这两个函数图象的另一交点B的坐标.
| x | -3 | 0 | 3 | 5 |
| y | -4 | 2 | 8 | 12 |
(2)已知点A(-2,-2)既在这个一次函数图象上,也在反比例函数y=$\frac{m}{x}$图象上,求这两个函数图象的另一交点B的坐标.
7.以下现象:①传送带上,瓶装饮料的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④在荡秋千的小朋友.其中属于平移的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
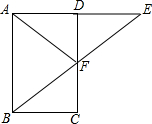 如图,矩形ABCD中,点E在线段AD延长线上,AD=DE,连接BE与DC相交于点F,连接AF,请从图中找出一个等腰三角形△AFE(答案不唯一).
如图,矩形ABCD中,点E在线段AD延长线上,AD=DE,连接BE与DC相交于点F,连接AF,请从图中找出一个等腰三角形△AFE(答案不唯一).
 如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过点B(3,0),C(4,3),将抛物线y=ax2+bx+3向上平移,使顶点E落在平移,使顶点E落在x轴上的点F处,则由两条抛物线、线段EF和y轴围成的图形(图中阴影部分)面积S=2.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过点B(3,0),C(4,3),将抛物线y=ax2+bx+3向上平移,使顶点E落在平移,使顶点E落在x轴上的点F处,则由两条抛物线、线段EF和y轴围成的图形(图中阴影部分)面积S=2.