题目内容
13.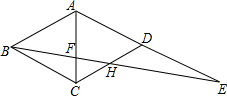 如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )| A. | 2 | B. | 3 | C. | $\frac{10}{3}$ | D. | $\frac{13}{3}$ |
分析 设DE=BF=x,CH=a,由CH∥AB,得$\frac{CH}{AB}$=$\frac{FH}{BF}$,推出ax=10,由CB∥DE,得$\frac{DE}{BC}$=$\frac{DH}{HC}$,得$\frac{x}{5}$=$\frac{5-x}{a}$,由此即可解决问题.
解答  解:设DE=BF=x,CH=a,
解:设DE=BF=x,CH=a,
∵四边形ABCD是菱形,
∴AB=CD=BC=AD=5,AB∥CD,AD∥BC,
∵CH∥AB,
∴$\frac{CH}{AB}$=$\frac{FH}{BF}$,
∴$\frac{a}{5}$=$\frac{2}{x}$,
∴ax=10,
∵CB∥DE,
∴$\frac{DE}{BC}$=$\frac{DH}{HC}$,
∴$\frac{x}{5}$=$\frac{5-x}{a}$,
∴ax=25-5x,
∴5x=15,
∴x=3,
∴DE=3.
故选B.
点评 本题考查菱形的性质、平行线分线段成比例定理等知识,解题的关键是灵活运用平行线分线段成比例定理,学会设参数解决问题,体现了数形结合的思想,属于中考常考题型.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目

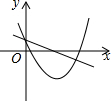
 如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过点B(3,0),C(4,3),将抛物线y=ax2+bx+3向上平移,使顶点E落在平移,使顶点E落在x轴上的点F处,则由两条抛物线、线段EF和y轴围成的图形(图中阴影部分)面积S=2.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过点B(3,0),C(4,3),将抛物线y=ax2+bx+3向上平移,使顶点E落在平移,使顶点E落在x轴上的点F处,则由两条抛物线、线段EF和y轴围成的图形(图中阴影部分)面积S=2.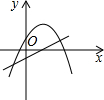
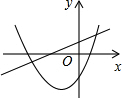
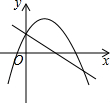
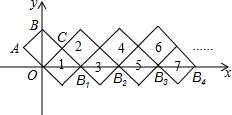 如图,在平面直角坐标系中放置一正方形OABC,OA=1,点B在y轴上,正方形1,2,3…是由正方形OABC通过某种变化得到的,正方形的顶点B1,B2,B3,…都在x轴上,按此规律,第n个正方形右侧顶点的横坐标是$\frac{n+1}{2}$$\sqrt{2}$.
如图,在平面直角坐标系中放置一正方形OABC,OA=1,点B在y轴上,正方形1,2,3…是由正方形OABC通过某种变化得到的,正方形的顶点B1,B2,B3,…都在x轴上,按此规律,第n个正方形右侧顶点的横坐标是$\frac{n+1}{2}$$\sqrt{2}$.