题目内容
16. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则线段ON的长为1.
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=2,则线段ON的长为1.
分析 作MH⊥AC于H,如图,根据正方形的性质得∠MAH=45°,则△AMH为等腰直角三角形,再求出AH,MH,MB,CH/CO,然后证明△CON∽△CHM,再利用相似比可计算出ON的长
解答 解:作MH⊥AC于H,如图,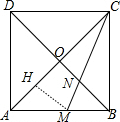
∵四边形ABCD为正方形,
∴∠MAH=45°,
∴△AMH为等腰直角三角形,
∴AH=MH=$\frac{\sqrt{2}}{2}$AM=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,
∵CM平分∠ACB,
∴BM=MH=$\sqrt{2}$,
∴AB=2+$\sqrt{2}$,
∴AC=$\sqrt{2}$AB=2$\sqrt{2}$+2,
∴OC=$\frac{1}{2}$AC=$\sqrt{2}$+1,CH=AC-AH=2$\sqrt{2}$+2-$\sqrt{2}$=2+$\sqrt{2}$,
∵BD⊥AC,
∴ON∥MH,
∴△CON∽△CHM,
∴$\frac{ON}{MH}$=$\frac{OC}{CH}$,即$\frac{ON}{\sqrt{2}}$=$\frac{\sqrt{2}+1}{2+\sqrt{2}}$,
∴ON=1.
故答案为1.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了角平分线的性质和正方形的性质.

练习册系列答案
相关题目
7.以下现象:①传送带上,瓶装饮料的移动;②打气筒打气时,活塞的运动;③钟摆的摆动;④在荡秋千的小朋友.其中属于平移的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
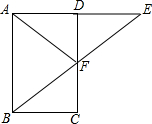 如图,矩形ABCD中,点E在线段AD延长线上,AD=DE,连接BE与DC相交于点F,连接AF,请从图中找出一个等腰三角形△AFE(答案不唯一).
如图,矩形ABCD中,点E在线段AD延长线上,AD=DE,连接BE与DC相交于点F,连接AF,请从图中找出一个等腰三角形△AFE(答案不唯一). 如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过点B(3,0),C(4,3),将抛物线y=ax2+bx+3向上平移,使顶点E落在平移,使顶点E落在x轴上的点F处,则由两条抛物线、线段EF和y轴围成的图形(图中阴影部分)面积S=2.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过点B(3,0),C(4,3),将抛物线y=ax2+bx+3向上平移,使顶点E落在平移,使顶点E落在x轴上的点F处,则由两条抛物线、线段EF和y轴围成的图形(图中阴影部分)面积S=2. 如图,AB是⊙O的直径,AB=2,CD与⊙O相切于点D,∠DAB=60°,点E在切线CD上,则当∠AEB最大时,AE=1.
如图,AB是⊙O的直径,AB=2,CD与⊙O相切于点D,∠DAB=60°,点E在切线CD上,则当∠AEB最大时,AE=1.