题目内容
12.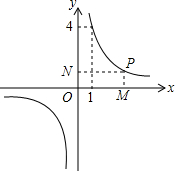 如图所示,P是反比例函数y=$\frac{k}{x}$的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为M,N.
如图所示,P是反比例函数y=$\frac{k}{x}$的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为M,N.(1)求k的值;
(2)求证:矩形OMPN的面积为定值.
分析 (1)由反比例函数y=$\frac{k}{x}$的图象上一点的坐标为(1,4),即可得到结论;
(2)根据反比例函数系数k的几何意义得到:矩形PAOB的面积为|k|.
解答 解:(1)如图,∵反比例函数y=$\frac{k}{x}$的图象上一点的坐标为(1,4),
∴k=4×1=4;
(2)∵k=4,
∴反比例函数的解析式为:y=$\frac{4}{x}$,
∵P是反比例函数y=$\frac{k}{x}$的图象上任意一点,
PM⊥x轴,PN⊥y轴,
∴矩形OMPN的面积=|k|=4,
∴矩形OMPN的面积为定值
点评 本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 解不等式$\frac{1}{2}(x+1)≤\frac{2}{3}x-1$,并把它的解集表示在数轴上,再写出它的最小整数解.
解不等式$\frac{1}{2}(x+1)≤\frac{2}{3}x-1$,并把它的解集表示在数轴上,再写出它的最小整数解.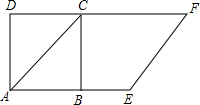 如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.
如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE=AC,以AE为一边作菱形AEFC,若菱形的面积为9$\sqrt{2}$cm2,则正方形ABCD的面积为9.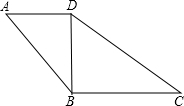 如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.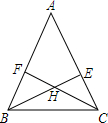 已知:如图,BE和CF是△ABC的高线,BE=CF,H是CF、BE的交点.求证:HB=HC.
已知:如图,BE和CF是△ABC的高线,BE=CF,H是CF、BE的交点.求证:HB=HC.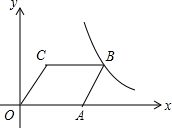 如图,?OABC的边OA在x轴上,C(1,2),A(3,0),双曲线y=$\frac{k}{x}$(x>0)经过点B,求k的值.
如图,?OABC的边OA在x轴上,C(1,2),A(3,0),双曲线y=$\frac{k}{x}$(x>0)经过点B,求k的值.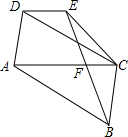 如图,在?ABCD中,过点B作BE交对角线AC于点F,且BF=EF,连接DE、CE,求证:AC∥DE.
如图,在?ABCD中,过点B作BE交对角线AC于点F,且BF=EF,连接DE、CE,求证:AC∥DE.