题目内容
10.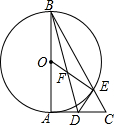 如图,△ABC中.△BAC=90°,以AB为直径作⊙O交BC于E,D为AC的中点,连结DE.
如图,△ABC中.△BAC=90°,以AB为直径作⊙O交BC于E,D为AC的中点,连结DE.(1)求证:DE是⊙O的切线;
(2)连BD交OE于F,若AB=10,OF=2,求tan∠BFO.
分析 (1)连接OD,证AD=DE,证△OAD≌△OED,∠OED=∠OAD=90°即可.
(2)连接AE,由OF=2,OE=5可求EF=3,设DO=2k,BE=3k,则BC=4k,EC=k,可求AC=2k,由勾股定理解得AD,得出DE,即可得出tan∠BFO.
解答 (1)证明:连接OD;如图1所示: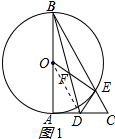
∵O、D分别是AB、AC的中点,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOE=∠BEO;
∵OB=OE,
∴∠AOD=∠DOE,
在△OAD和△OED中,$\left\{\begin{array}{l}{OA=OE}&{\;}\\{∠AOD=∠DOE}&{\;}\\{OD=OD}&{\;}\end{array}\right.$,
∴△OAD≌△OED(SAS),
∴∠OED=∠OAD=90°,DE=AD,
∴DE为⊙O的切线.
(2)解:连接AE,如图2所示: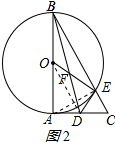
∵OF=2,OE=5
∴EF=3;
∵OD∥BC,OD=$\frac{1}{2}$BC,
∴OD:BE=OF:EF=2:3;
设DO=2k,BE=3k,
则BC=4k,EC=k,
∵OD∥BC,
∴∠ODA=∠C,
又∠OAD=∠AEC=90°,
∴△OAD∽△EAC,
设AD=x,则AC=2k,
∴$\frac{AD}{EC}=\frac{OD}{AC}$,即$\frac{x}{k}=\frac{2k}{2x}$,
∴x=k,则AC=2x=2k,
又AB2+AC2=BC2,
即102+(2k)2=(4k)2,
解得:k=$\frac{5\sqrt{3}}{3}$,
∴DE=AD=$\frac{5\sqrt{3}}{3}$,
∴tan∠BFO=tan∠DFE=$\frac{DE}{EF}$=$\frac{\frac{5\sqrt{3}}{3}}{3}$=$\frac{5\sqrt{3}}{9}$.
点评 本题考查了切线的判定,勾股定理和三角形全等的判定,三角函数,相似三角形的判定与性质等知识点.熟练掌握切线的判定,由勾股定理求出AD是解决问题(2)的关键.

| A. |  | B. |  | C. |  | D. |  |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
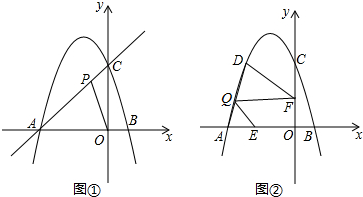
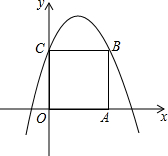 如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.
如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.