题目内容
17.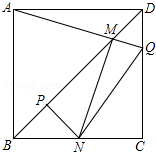 如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.
如图,边长一定的正方形ABCD,Q为CD上一个动点,AQ交BD于点M,过M作MN⊥AQ交BC于点N,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;②MP=$\frac{1}{2}$BD;③BN+DQ=NQ;④$\frac{AB+BN}{BM}$为定值.其中一定成立的是①②③④.
分析 由题意可知A,B,N,M四点共圆,进而可得出∠ANM=∠NAM=45°,由等角对等边知,AM=MN,故①正确;
由同角的余角相等知,∠HAM=∠PMN,所以Rt△AHM≌Rt△MPN,即可得出结论,故②正确;
先由题意得出四边形SMWB是正方形,进而证出△AMS≌△NMW,因为AS=NW,所以AB+BN=SB+BW=2BW,而BW:BM=1:$\sqrt{2}$,得出$\frac{AB+BN}{BM}$═$\sqrt{2}$,故④正确.
因为∠BAN+∠QAD=∠NAQ=45°,在∠NAM作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,所以△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ=90°,BN=NU,DQ=UQ,即可得出结论,故③正确;
解答 解:如图1所示: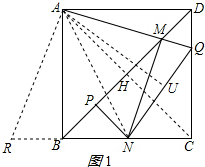
作AU⊥NQ于U,连接AN,AC,
∵∠AMN=∠ABC=90°,
∴A,B,N,M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴AM=MN,故①正确.
由同角的余角相等知,∠HAM=∠PMN,
在△AHM和△MPN中,
$\left\{\begin{array}{l}{∠AHM=∠MPN}&{\;}\\{∠HAM=∠PMN}&{\;}\\{AM=MN}&{\;}\end{array}\right.$,
∴△AHM≌△MPN(AAS),
∴MP=AH=$\frac{1}{2}$AC=$\frac{1}{2}$BD,故②正确,
∵∠BAN+∠QAD=∠NAQ=45°,
∴△ADQ绕点A顺时针旋转90度至△ABR,使AD和AB重合,连接AN,
则∠RAQ=90°,△ABR≌△ADQ,
∴AR=AQ,∠RAN=90°-45°=45°=∠NAM,
在△△AQN和△ANR中,
$\left\{\begin{array}{l}{AQ=AR}&{\;}\\{∠NAM=∠RAN}&{\;}\\{AN=AN}&{\;}\end{array}\right.$,
∴△AQN≌△ANR(SAS),
∴NR=NQ,
则BN=NU,DQ=UQ,
∴点U在NQ上,有BN+DQ=QU+UN=NQ,故③正确.
如图2所示,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,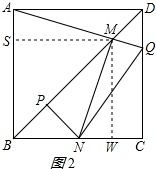 ∴四边形SMWB是正方形,
∴四边形SMWB是正方形,
∴MS=MW=BS=BW,∠SMW=90°,
∴∠AMS=∠NMW,
在△AMS和△NMW中,
$\left\{\begin{array}{l}{∠ASM=∠NWM}&{\;}\\{MS=MW}&{\;}\\{∠AMS=∠NMW}&{\;}\end{array}\right.$,
∴△AMS≌△NMW(ASA),
∴AS=NW,
∴AB+BN=SB+BW=2BW,
∵BW:BM=1:$\sqrt{2}$,
∴$\frac{AB+BN}{BM}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,故④正确.
故答案为:①②③④.
点评 本题考查了正方形的性质,四点共圆的判定,圆周角定理,等腰直角三角形的性质,全等三角形的判定和性质;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案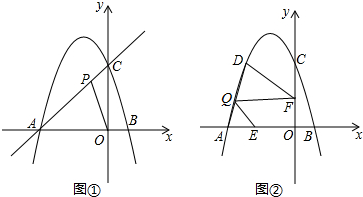
 如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.
如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.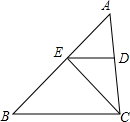 如图,∠AEC=70°,∠B=35°,EF平分∠AEC,试说明ED∥BC.
如图,∠AEC=70°,∠B=35°,EF平分∠AEC,试说明ED∥BC.