题目内容

14．化简：$\frac{2a}{{a}^{2}-4}$÷（$\frac{{a}^{2}}{a-2}$-a），然后在0，1，2，-2中选一个合适的值代入求值．

分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a=1代入计算即可求出值．

解答 解：原式=$\frac{2a}{（a+2）（a-2）}$÷（$\frac{{a}^{2}}{a-2}-\frac{{a}^{2}-2a}{a-2}$）
=$\frac{2a}{（a+2）（a-2）}$÷$\frac{2a}{a-2}$
=$\frac{2a}{（a+2）（a-2）}$×$\frac{a-2}{2a}$
=$\frac{1}{a+2}$，
当a=1时，原式=$\frac{1}{1+2}$=$\frac{1}{3}$．

点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
4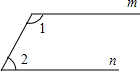．如图，若m∥n，∠1=105°，则∠2=（　　）
A．75°B．85°C．95°D．105°
5．下列图案中，既是中心对称图形又是轴对称图形的有（　　）
A．1个B．2个C．3个D．4个
2．解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x-1≤0}\\{-3x＜9}\end{array}\right.$．
9．已知五张卡片上分别写有五个数-2、-1、0、1、2，它们除数字不同外其余全部相同，先从中随机抽取一张，将抽到的卡片上的数字记为x，不放回再从剩下的随机抽取一张记为y，则点（x，y）落在两条直线y=x+3、y=-3x+3与x轴围成的区域内（包括边界）的概率为$\frac{2}{5}$．
5．如图，抛物线y=-x2+bx+c与x轴交于点A，B（1，0），与y轴交于点C（0，3）．
（1）求抛物线的解析式；
（2）如图①，点P在直线AC上，若S△PAO：S△PCO=2：1，求P点坐标；
（3）如图②，若点C关于对称轴对称的点为D，点E的坐标为（-2，0），F是OC的中点，连接DF，Q为线段AD上的一点，若∠EQF=∠ADF，求线段EQ的长．
12．如图①，在四边形AOBC中，AC∥OB，若动点P从点O处以每秒1个单位长度的速度向B点平移，过点P作垂直于OB的直线，设直线扫过的阴影部分的面积为S，运动时间为x（t），已知S与x的函数关系可用如图②的函数图象表示．
（1）求出图②中a、b的值；
（2）连接AP，在运动过程中是否存在某个时间x使得△OAP为等腰三角形？如果存在，求出此时x的值；如果不存在，请说明理由．
9．计算：
（1）$\frac{\sqrt{75}-\sqrt{3}}{\sqrt{3}}$-$\sqrt{\frac{1}{5}}$×$\sqrt{20}$  
（2）$\left\{\begin{array}{l}{3（x+y）-4（x-y）=4}\\{\frac{x+y}{2}+\frac{x-y}{6}=1}\end{array}\right.$ 
（3）$\left\{\begin{array}{l}{5x-1＜3（x+1）}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1}\end{array}\right.$．
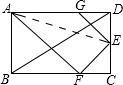10．如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处（AE为折痕，点E在CD上），在AD上截取DG，使以DG=CF．
（1）求证：△ABF∽△FCE；
（2）求证：BD⊥GE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网