题目内容
9.解不等式组$\left\{\begin{array}{l}{2x+1>3}\\{\frac{x+3}{5}≤\frac{2x-5}{3}-1}\end{array}\right.$,并把不等式组的解集在数轴上表示.分析 先求出两个不等式的解集,再将两不等式解集表示在数轴上,结合数轴求其公共解.
解答 解:解不等式2x+1>3,得:x>1,
解不等式$\frac{x+3}{5}≤\frac{2x-5}{3}-1$,得:x≥7,
把它们的解集在数轴上表示为:
所以,此不等式组的解集为:x≥7.
点评 本题主要考查解不等式组的能力,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了或者借助数轴确定解集的公共部分.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
4.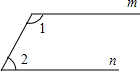 如图,若m∥n,∠1=105°,则∠2=( )
如图,若m∥n,∠1=105°,则∠2=( )
 如图,若m∥n,∠1=105°,则∠2=( )
如图,若m∥n,∠1=105°,则∠2=( )| A. | 75° | B. | 85° | C. | 95° | D. | 105° |
18.下列基本图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
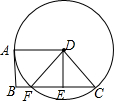 已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.
已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.