题目内容
19. 如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,且∠ACB=∠DCE,求证:CE是⊙O的切线.
如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,且∠ACB=∠DCE,求证:CE是⊙O的切线.
分析 连接OE,根据矩形的性质求出∠CAE=∠BCA=∠DCE,求出∠DCE+∠CED=90°,即可求出∠AEO+∠CED=90°,求出∠OEC=90°,根据切线的判定推出即可.
解答 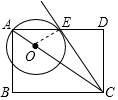 证明:连接OE,
证明:连接OE,
∵OA=OE,
∴∠CAD=∠OEA,
∵四边形ABCD是矩形,
∴∠D=90°,BC∥AD,
∴∠BCA=∠CAD,
∵∠ACB=∠DCE,
∴∠CAE=∠DCE,
∵∠DCE+∠CEB=180°-∠D=90°,
∴∠OEA+∠CED=90°,
∴∠OEC=180°-90°=90°,
∴CE是⊙O的切线.
点评 本题考查了矩形的性质,切线的判定的应用,解此题的关键是能正确作出辅助线,题目比较好,难度适中.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.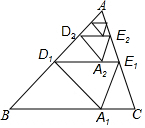 如图,对△ABC纸片进行如下操作:
如图,对△ABC纸片进行如下操作:
第1次操作:将△ABC沿着过AB中点D1的直线折叠,使点A落在BC边上的A1处,折痕D1E1到BC的距离记作h1,然后还原纸片;
第2次操作:将△AD1E1沿着过AD1中点D2的直线折叠,使点A落在D1E1边上的A1处,折痕D1E1到BC的距离记作h2,然后还原纸片;
…
按上述方法不断操作下去…,经过第n次操作后得到的折痕DnEn到BC的距离记作hn,若h=1,则hn的值不可能是( )
 如图,对△ABC纸片进行如下操作:
如图,对△ABC纸片进行如下操作:第1次操作:将△ABC沿着过AB中点D1的直线折叠,使点A落在BC边上的A1处,折痕D1E1到BC的距离记作h1,然后还原纸片;
第2次操作:将△AD1E1沿着过AD1中点D2的直线折叠,使点A落在D1E1边上的A1处,折痕D1E1到BC的距离记作h2,然后还原纸片;
…
按上述方法不断操作下去…,经过第n次操作后得到的折痕DnEn到BC的距离记作hn,若h=1,则hn的值不可能是( )
| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{13}{8}$ | D. | $\frac{31}{16}$ |
8.计算:
(1)(-1)2017-23+(cos68°+$\frac{5}{π}$)0+|3$\sqrt{3}$-8sin60°|;
(2)$\sqrt{2}$cos45°-tan30°•sin60°.
(1)(-1)2017-23+(cos68°+$\frac{5}{π}$)0+|3$\sqrt{3}$-8sin60°|;
(2)$\sqrt{2}$cos45°-tan30°•sin60°.
6.若k为正整数,则2•(-2)2k+(-2)2k+1等于( )
| A. | 0 | B. | 22k+1 | C. | -22k+1 | D. | 22k+2 |