题目内容

2．若（2x-1）6=a0x6+a1x5+a2x4+a3x3+a4x2+a5x+a6，则a1+a3+a5的值-364．

分析 由题意（2x-1）6=a0x6+a1x5+a2x4+a3x3+a4x2+a5x+a6，可以令x=±1分别代入其中得到两个等式，然后让两式相减，即可求解．

解答 解：∵（2x-1）6=a0x6+a1x5+a2x4+a3x3+a4x2+a5x+a6，
令x=1得，（2-1）6=a0+a1+a2+a3+a4+a5+a6，
∴a0+a1+a2+a3+a4+a5+a6=1，①
令x=-1得，（-2-1）6=a0-a1+a2-a3+a4-a5+a6，
∴a0-a1+a2-a3+a4-a5+a6=（-3）6=729，②
①-②得：2（a1+a3+a5）=-728，
∴a1+a3+a5=-364．
故答案为：-364．

点评 此题主要考查代数式求解，解题的关键是取特值法，即令x=±1，然后求解．

练习册系列答案
相关题目
12．若两个相似三角形的相似比是2：3，则它们的对应高线的比是2：3．
13．如图（1），已知抛物线y=ax2+bx+5与x轴交于A、B（点A在点B的左侧）两点，与y轴交于点C，已知点A的横坐标为-5，且点D（-2，-3）在此抛物线的对称轴上．
（1）求a、b的值；
（2）若在直线AC上方的抛物线上有一点M，当点M到x轴的距离与M到直线AC的距离之比为$\frac{{4\sqrt{2}}}{3}$时，在y轴上找一点P，使得|PD-PM|值最大，时求此时点P的坐标及|PD-PM|的最大值；
（3）如图（2），过点B作BK⊥x轴交直线AC于点K，连接DK、AD，点H是DK的中点，点G是线段AK上任意一点，将△DGH沿边GH翻折得△D'GH，当KG为何值时，△D'GH与△KGH重叠部分的面积是△DGK面积的$\frac{1}{4}$？
10．解方程组：$\left\{\begin{array}{l}{x+y+z=6}\\{3x-y+2z=12}\\{x-y-3z=-4}\end{array}\right.$．
17．已知$\root{3}{374}$≈7.205，$\root{3}{37.4}$≈3.344，则$\root{3}{-0.000374}$约等于（　　）
A．-0.07205B．-0.03344C．-0.07205D．-0.003344
7．斐波那契（约1170-1250，意大利数学家）数列是按某种规律排列的一列数，他发现该数列中的每个正整数都可以用无理数的形式表示，如第n（n为正整数）个数an可表示为$\frac{1}{\sqrt{5}}$[（$\frac{1+\sqrt{5}}{2}$）n-（$\frac{1-\sqrt{5}}{2}$）n]．
（1）计算第一个数a1；
（2）计算第二个数a2；
（3）证明连续三个数之间an-1，an，an+1存在以下关系：an+1-an=an-1（n≥2）；
（4）写出斐波那契数列中的前8个数．
14．在平面直角坐标系中，直线y=$\frac{1}{2}$x+2分别与x轴，y轴交于A、B两点，过点C（1，0）的直线l∥AB．
（1）请直接写出A、B两点的坐标；并求AB的长度；
（2）求直线l的函数关系式；
（3）已知：动点P在线段BC 上，AD⊥AP交直线l于D点．连结DP，试探索：在P点的运动过程中，∠ADP的大小是否会发生变化？为什么？
11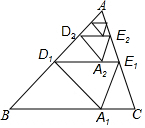．如图，对△ABC纸片进行如下操作：
第1次操作：将△ABC沿着过AB中点D1的直线折叠，使点A落在BC边上的A1处，折痕D1E1到BC的距离记作h1，然后还原纸片；
第2次操作：将△AD1E1沿着过AD1中点D2的直线折叠，使点A落在D1E1边上的A1处，折痕D1E1到BC的距离记作h2，然后还原纸片；
…
按上述方法不断操作下去…，经过第n次操作后得到的折痕DnEn到BC的距离记作hn，若h=1，则hn的值不可能是（　　）
A．$\frac{3}{2}$B．$\frac{7}{4}$C．$\frac{13}{8}$D．$\frac{31}{16}$
9．计算：6ab（2a+3b）=12a2b+18ab2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网