题目内容
19. 如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的Bˊ点,AE是折痕.
如图,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的Bˊ点,AE是折痕.(1)试判断BˊE与DC的位置关系.
(2)如果∠C=140°,求∠AEB的度数.
分析 (1)根据翻折的性质,可得∠AB′E,根据平行线的判定;
(2)根据四边形的性质,可得∠DAB的度数,根据翻折的性质,可得答案.
解答 解:(1)由折叠的性质,得
∠B=∠AB′E=90°,
∴∠AB′E=∠C=90°,
∴B′E∥DC;
(2)由四边形的一组对角互补,得
∠DAB+∠C=180°.
由∠C=140°得
∠DAB=180°-∠C=40°.
由翻折的性质,得
∠BAE=$\frac{1}{2}$∠DAB=$\frac{1}{2}$×40°=20°.
点评 本题考查了翻折的性质,利用翻折的性质得出∠B=∠AB′E=90°是解题关键.

练习册系列答案
相关题目
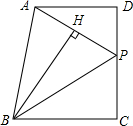 如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD
如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD


 如图,在△ABC中,AB=AC,AD是中线,CE∥AD交BA的延长线于点E,请判断△AEC的形状,并说明理由.
如图,在△ABC中,AB=AC,AD是中线,CE∥AD交BA的延长线于点E,请判断△AEC的形状,并说明理由.