题目内容
7.设直线kx+(k+1)y-1=0与坐标轴所围成的直角三角形的面积为Sk,则S1+S2+…+S2017=$\frac{2017}{4036}$.分析 利用一次函数图象上点的坐标特征可求出直线kx+(k+1)y-1=0与坐标轴的交点坐标,根据三角形的面积公式可得出Sk=$\frac{1}{2}$($\frac{1}{k}$-$\frac{1}{k+1}$),将其代入S1+S2+…+S2017中,即可求出结论.
解答 解:当x=0时,有(k+1)y-1=0,
解得:y=$\frac{1}{k+1}$,
∴直线kx+(k+1)y-1=0与y轴交点坐标为(0,$\frac{1}{k+1}$);
当y=0时,有kx-1=0,
解得:x=$\frac{1}{k}$,
∴直线kx+(k+1)y-1=0与x轴的交点坐标为($\frac{1}{k}$,0).
∴Sk=$\frac{1}{2}$$\frac{1}{k}$•$\frac{1}{k+1}$=$\frac{1}{2}$($\frac{1}{k}$-$\frac{1}{k+1}$),
∴S1+S2+…+S2017=$\frac{1}{2}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2017}$-$\frac{1}{2018}$)=$\frac{1}{2}$(1-$\frac{1}{2018}$)=$\frac{2017}{4036}$.
故答案为:$\frac{2017}{4036}$.
点评 本题考查了一次函数图象上点的坐标特征以及三角形的面积,利用一次函数图象上点的坐标特征结合三角形的面积找出Sk=$\frac{1}{2}$($\frac{1}{k}$-$\frac{1}{k+1}$)是解题的关键.

练习册系列答案
相关题目
18.已知方程组$\left\{\begin{array}{l}{bx+ay=3}\\{ax-by=-1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,求a,b的值( )
| A. | $\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ |
15.下列有关相反数的说法:①符号相反的数叫相反数;②数轴上原点两旁的数是相反数;③-(-3)的相反数是-3;④-a一定是负数;⑤)若两个数之和为0,则这两个数互为相反数; ⑥若两个数互为相数,则这两个数一定是一个正数一个负数.其中正确的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.若分式$\frac{|x|-3}{x-3}$的值为零,则x的值应取( )
| A. | x=3 | B. | x=-3 | C. | x=±3 | D. | x=0 |
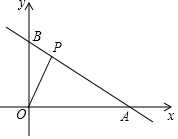 直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).
直线y=kx+6与x轴、y轴分别交于A、B两点,点A的坐标为(8,0).